题目内容
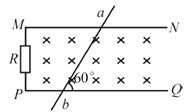
【题目】如图所示，两根足够长的光滑平行金属导轨MN、PQ间距为l＝0.5m，其电阻不计，两导轨及其构成的平面均与水平面成30°角。完全相同的两金属棒ab、cd分别垂直导轨放置，每棒两端都与导轨始终有良好接触。已知两棒质量均为m＝0.02kg，电阻均为R＝0.1Ω，整个装置处在垂直于导轨平面向上的匀强磁场中，磁感应强度B＝0.2T，棒ab在平行于导轨向上的力F作用下，沿导轨向上匀速运动，而棒cd恰好能够保持静止。取g＝10m/s2，求：
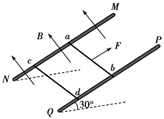
(1)通过棒cd的电流I是多少，方向如何？
(2)棒ab受到的力F多大？
(3)棒cd每产生Q＝0.1J的热量，力F做的功W是多少？
【答案】(1)I＝1A, 方向由d至c (2)F＝0.2N (3) W＝0.4J
【解析】(1)棒cd受到的安培力为： 
①
棒cd在共点力作用下平衡，则： 
②
由①②式，代入数据解得： 
③
根据楞次定律可知，棒cd中的电流方向由d至c ④
(2)棒ab与棒cd受到的安培力大小相等，即： 
对棒ab，由共点力平衡知： 
⑤
代入数据解得： 
⑥
(3)设在时间t内棒cd产生
的热量，由焦耳定律知： 
Rt ⑦
设棒ab匀速运动的速度大小为v，其产生的感应电动势为： 
⑧
由闭合电路欧姆定律知： 
⑨
由运动学公式知在时间t内，棒ab沿导轨的位移为： 
⑩
力F做的功为： 
综合上述各式，代入数据解得： 
。
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
