题目内容
10. 质量m=2.0kg的小铁块静止于水平导轨AB的A端,导轨及支架ABCD形状及尺寸如图所示,它只能绕通过支架D点的垂直于纸面的水平轴转动,其重心在图中的O点,质量M=4.0kg,现用一细线沿导轨拉铁块,拉力F=12N,铁块和导轨之间的动摩擦因数μ=0.50.重力加速度g=10m/s2,求:
质量m=2.0kg的小铁块静止于水平导轨AB的A端,导轨及支架ABCD形状及尺寸如图所示,它只能绕通过支架D点的垂直于纸面的水平轴转动,其重心在图中的O点,质量M=4.0kg,现用一细线沿导轨拉铁块,拉力F=12N,铁块和导轨之间的动摩擦因数μ=0.50.重力加速度g=10m/s2,求:(1)铁块启动时的加速度?
(2)从铁块运动时起,导轨(及支架)能保持静止的最长时间是多少?
分析 (1)小铁块刚开始运动时受到重力、导轨的支持力和摩擦力、水平拉力F作用,重力与支持力平衡,根据牛顿第二定律求出加速度.
(2)导轨和支架始终保持静止,小铁块是先做匀加速直线运动,再做匀减速直线运动,位移之和等于第(2)问所求距离.根据牛顿第二定律求出两个过程的加速度,利用位移关系求解拉力F作用的最长时间.
解答 解:(1)铁块受的摩擦力f=μmg=×0.5×20N=10N,向左,由牛顿第二定律得:
F-f=ma
代入得:12-10=2a,
得:a=1m/s2;
(2)导轨刚要不能维持平衡时,C端受的力为零,此时导轨(及支架)除转轴之外共受三个力:滑块对导轨的压力N=mg,竖直向下;
滑块对导轨的摩擦力f=μmg=10N,方向向右;重力Mg,作用在O点,方向竖直向下.设此时铁块走过路程为S,根据力矩平衡条件及图中尺寸,可得:
Mg×0.1+mg(0.7-s)=f×0.8=μmg×0.8
代入得:40×0.1+20(0.7-s)=10×0.8
解得:S=0.50(m)
由 S=$\frac{1}{2}a{t}^{2}$,
得:t=$\sqrt{\frac{2S}{a}}$=$\sqrt{\frac{2×0.5}{1}}$=1s
答:(1)铁块启动时的加速度是1m/s2.
(2)从铁块运动时起,导轨(及支架)能保持静止的最长时间是1s.
点评 本题是力矩平衡与牛顿定律、公式规律的综合应用.在第(2)问中列力矩平衡方程时摩擦力的力矩不能遗漏.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
1.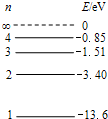 氢原子部分能级的示意图如图所示,不同色光的光子能量如表所示:
氢原子部分能级的示意图如图所示,不同色光的光子能量如表所示:
处于某激发态的氢原子,发射的光的谱线在可见光范围内仅有2条,其颜色分别为( )
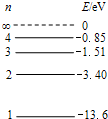 氢原子部分能级的示意图如图所示,不同色光的光子能量如表所示:
氢原子部分能级的示意图如图所示,不同色光的光子能量如表所示:| 色光光子 能量范围 (eV) | 红 | 橙 | 黄 | 绿 | 蓝-靛 | 紫 |
| 1.61~2.00 | 2.00~2.07 | 2.07~2.14 | 2.14~2.53 | 2.53~2.76 | 2.76~3.10 |
| A. | 黄、绿 | B. | 红、紫 | C. | 红、蓝-靛 | D. | 蓝-靛、紫 |
5.下列说法正确的是( )
| A. | 汤姆孙发现电子后猜想出原子内的正电荷集几在在很小的核内 | |
| B. | 原子的核式结构模型很好地解释了氢原子光谱 | |
| C. | 氢原子从低能级向高能级跃迁时产生原子光谱 | |
| D. | 在α、β、γ这三种射线中,γ射线的穿透能力最强,α射线的电离能力最强 |
15.关于电磁波谱,下列说法中正确的是( )
| A. | 红外线比红光波长长,它的热作用很强 | |
| B. | X射线就是伦琴射线 | |
| C. | 阴极射线是一种频率极高的电磁波 | |
| D. | 紫外线的波长比伦琴射线长,它的显著作用是荧光作用 |
 如图是为了检验某种防护罩承受冲击力的装置,M是半径为R=1.0m的固定于竖直平面内的$\frac{1}{4}$光滑圆弧轨道,轨道上端切线水平.N为待检验的固定曲面,该曲面在竖直面内的截面为半径r=$\sqrt{0.69}$m的$\frac{1}{4}$圆弧,圆弧下端切线水平且圆心恰好位于M轨道的上端点P.M的下端相切处放置竖直向上的弹簧枪,可发射速度不同的质量m=0.1kg的小钢珠.假设某次发射的钢珠沿轨道恰好能过P点,水平飞出后落到曲面N的某一点上,取g=10m/s2.求:(计算结果可以用根号表示)
如图是为了检验某种防护罩承受冲击力的装置,M是半径为R=1.0m的固定于竖直平面内的$\frac{1}{4}$光滑圆弧轨道,轨道上端切线水平.N为待检验的固定曲面,该曲面在竖直面内的截面为半径r=$\sqrt{0.69}$m的$\frac{1}{4}$圆弧,圆弧下端切线水平且圆心恰好位于M轨道的上端点P.M的下端相切处放置竖直向上的弹簧枪,可发射速度不同的质量m=0.1kg的小钢珠.假设某次发射的钢珠沿轨道恰好能过P点,水平飞出后落到曲面N的某一点上,取g=10m/s2.求:(计算结果可以用根号表示)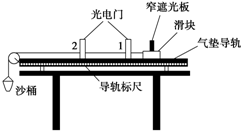 某学习小组在“研究匀变速直线运动”的实验中,用如图所示的气垫导轨装置来测小车的加速度,由导轨标尺可以测出两个光电门之间的距离L,窄遮光板的宽度为d,窄遮光板依次通过两个光电门的时间分别为t1、t2.
某学习小组在“研究匀变速直线运动”的实验中,用如图所示的气垫导轨装置来测小车的加速度,由导轨标尺可以测出两个光电门之间的距离L,窄遮光板的宽度为d,窄遮光板依次通过两个光电门的时间分别为t1、t2. 如图所示,一段直光导纤维,折射率为n,长为L.光在真空中的速度为c,求:
如图所示,一段直光导纤维,折射率为n,长为L.光在真空中的速度为c,求: 如图所示,两个天体构成双星,绕同一点做圆周运动,两星中心的距离为L,转动的周期为T,其中一颗星球质量为m,则另一颗星球质量为$\frac{{L}^{3}4{π}^{2}}{G{T}^{2}}$.(已知万有引力常量为G.)
如图所示,两个天体构成双星,绕同一点做圆周运动,两星中心的距离为L,转动的周期为T,其中一颗星球质量为m,则另一颗星球质量为$\frac{{L}^{3}4{π}^{2}}{G{T}^{2}}$.(已知万有引力常量为G.)