题目内容
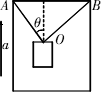
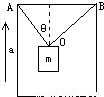
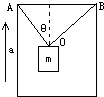如图所示的升降机中，用OA、OB两根绳子吊一个质量为20kg的重物，若OA与竖直方向的夹角θ=37°OA垂直于OB，且两绳所能承受的最大拉力均为320N，为使绳子不断，升降机竖直向上的加速度最大为多少？
解：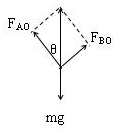
以物体为研究对象，作出力图，如图．升降机竖直向上做匀加速运动时，加速度竖直向上，合力一定竖直向上，则两根绳子的拉力的合力方向一定竖直向上．由力图可知，BO绳的拉力大于AO绳的拉力，当B绳的拉力达到最大时，升降机的加速度为最大．
根据牛顿第二定律得，
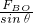-mg=mam，
代入解得 am=10m/s2
答：为使绳子不断，升降机竖直向上的加速度最大为10m/s2．
分析：以物体为研究对象，作出力图，分析AO、BO两绳拉力的大小，确定当升降机的加速度增大时，哪根绳子的拉力先达到最大．再根据牛顿第二定律求出加速度的最大值．
点评：本题是动力学中临界问题，分析临界条件是关键．当绳子刚要被拉断时，绳子的拉力达到最大值，是常用的临界条件．
以物体为研究对象，作出力图，如图．升降机竖直向上做匀加速运动时，加速度竖直向上，合力一定竖直向上，则两根绳子的拉力的合力方向一定竖直向上．由力图可知，BO绳的拉力大于AO绳的拉力，当B绳的拉力达到最大时，升降机的加速度为最大．根据牛顿第二定律得，
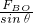-mg=mam，代入解得 am=10m/s2
答：为使绳子不断，升降机竖直向上的加速度最大为10m/s2．
分析：以物体为研究对象，作出力图，分析AO、BO两绳拉力的大小，确定当升降机的加速度增大时，哪根绳子的拉力先达到最大．再根据牛顿第二定律求出加速度的最大值．
点评：本题是动力学中临界问题，分析临界条件是关键．当绳子刚要被拉断时，绳子的拉力达到最大值，是常用的临界条件．
练习册系列答案
阅读快车系列答案
相关题目
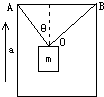如图所示的升降机中，用OA、OB两根绳子吊一个质量为20kg的重物，若OA与竖直方向的夹角θ=37°OA垂直于OB，且两绳所能承受的最大拉力均为320N，为使绳子不断，升降机竖直向上的加速度最大为多少？
＝37°，OA垂直于OB，且两绳所能承受的最大拉力均为320 N，为使绳子不断，升降机竖直向上的加速度最大为多少？(g取10 m/s2)
