Question

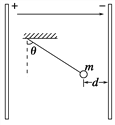
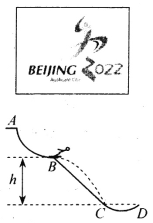
【题目】第24届冬季奥林匹克运动会，将于2022年2月4日在北京和张家口联合举行，北京也将成为奥运史上首个举办过夏季奥林匹克运动会和冬季奥林匹克运动会的城市。跳台滑雪是冬奥会中最具观赏性的项目之一，如图，跳台滑雪赛道由助滑道AB、着陆坡BC、停止区CD三部分组成；比赛中，质量为m的运动员从A处由静止下滑，运动到B处后水平飞出，落在了着陆坡末端的C点，滑入停止区后，在与C等高的D处速度减为零。B、C间的高度差为h，着陆坡的倾角为，重力加速度为g，不计运动员在助滑道AB受到的摩擦阻力及空气阻力，则

A.A、B间的高度差为

B.适当调节助滑道AB和着陆坡BC，运动员可以沿与BC相切的方向着陆

C.运动员在停止区CD上克服摩擦力所做的功为

D.当运动员飞出后，瞬时速度方向与水平方向间的夹角为θ时，其离着陆坡BC最远

Answer 1

【答案】AD

【解析】

A．设运动员在空中飞行的时间为t，根据平抛运动的规律有，解得

水平方向有：x=vBt，由几何关系可得：

=tanθ

代入数据解得运动员经过B点时速度为

vB=

从A到B由动能定理得：

mghAB=

解得：

故A正确。

B．设运动员着陆时速度方向与水平方向的夹角为α，则

由

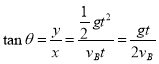
可得

tanα=2tanθ，α≠θ

与vB无关，所以，调节助滑道AB和着陆坡BC，运动员不可能沿与BC相切的方向着陆，故B错误；

C．设运动员在停止区CD上克服摩擦力所做的功为Wf。从B到D的过程由动能定理得：

可得

故C错误；

D．运动员飞出后做平抛运动，瞬时速度方向与着陆坡BC平行时，即瞬时速度方向与水平方向间的夹角为θ时，其离着陆坡BC最远，故D正确。

故选AD。