Question

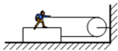如图所示，人重600N，木块重400N，人与木块间的滑动摩擦因数为0.5，木块与地面间的滑动摩擦因数为0.4，光滑滑轮固定在竖直墙上，现在人用水平力拉绳，使他与木块一起向右匀速运动，则（　　）

A．人拉绳的力是150N

B．人拉绳的力是400N

C．人拉绳的力是200N

D．人拉绳的力是300N

Answer 1

分析：以人和木块整体为研究对象，对整体进行受力分析，由共点力的平衡条件可求得绳子拉人的力，最后结合牛顿第三定律求解出人拉绳子的力．

解答：解：对人和绳子整体受力分析，受重力、支持力和两倍的拉力，如图

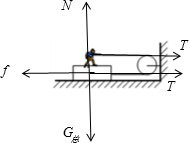
根据平衡条件，有
N=G_总   ①
2T=f  ②
其中
f=μ_地N   ③
由①②③解得
T=

1

2

μ地G总=

1

2

×0.4×(600+400)=200N
故选C．

点评：本题关键是对要选择整体为研究对象，受力分析后根据平衡条件列方程求解；如果分别对人和木块受力分析后列平衡方程求解，问题会复杂化．