题目内容
6.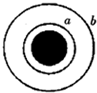 如图所示,“嫦娥一号”卫星分别在离月球较近的圆轨道a和离月球较远的圆轨道b上做匀速圆周运动.则该卫星( )
如图所示,“嫦娥一号”卫星分别在离月球较近的圆轨道a和离月球较远的圆轨道b上做匀速圆周运动.则该卫星( )| A. | 在轨道a上的周期大于在b上的周期 | |
| B. | 在轨道a上的加速度大于在b上的加速度 | |
| C. | 在轨道a上的线速度小于在b上的线速度 | |
| D. | 在轨道a上的角速度小于在b上的角速度 |
分析 卫星绕地球做圆周运动,万有引力提供向心力,由牛顿第二定律求出轨道半径、加速度、线速度与角速度,然后分析答题
解答 解:卫星绕地球做圆周运动,万有引力提供向心力;
A、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$({\frac{2π}{T})}^{2}$r,解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,由于ra<rb,则在轨道a上的周期小于在轨道b上的周期,故A错误;
B、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=ma,解得:a=$\frac{GM}{{r}^{2}}$,由于ra<rb,则在轨道a上的加速度大于在轨道b上的角速度,故B正确;
C、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,解得:v=$\sqrt{\frac{GM}{r}}$,由于ra<rb,则在轨道a上的线速度大于在轨道b上的线速度,故C错误;
D、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=mω2r,解得:ω=$\sqrt{\frac{GM}{{r}^{3}}}$,由于ra<rb,则在轨道a上的角速度大于在轨道b上的角速度,故D错误;
故选:B.
点评 本题考查了万有引力定律的应用,知道万有引力提供向心力,应用向心力公式、牛顿第二定律可以解题,本题是一道基础题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
16.一辆汽车匀速率通过一段凸凹不平的路面,分别通过A、B、C三个位置时( )
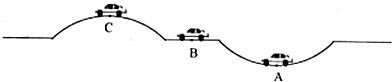

| A. | 汽车通过A位置时对路面的压力最大 | |
| B. | 汽车通过B位置时对路面的压力最大 | |
| C. | 汽车通过C位置时对路面的压力最大 | |
| D. | 汽车通过A、B、C位置时对路面的压力一样大 |
17.如图,时钟正常工作,比较时针、分针和秒针转动的角速度和周期,秒针的( )


| A. | 角速度最大,周期最大 | B. | 角速度最大,周期最小 | ||
| C. | 角速度最小,周期最大 | D. | 角速度最小,周期最小 |
14.一架飞机在距地面h高处以初速度v1水平匀速飞行,在地面正上方有一条水平公路,此时有一辆敌方的运送弹药的汽车正以速度v2相向行驶过来,则飞行员释放炸弹时应距汽车的直线距离为( )
| A. | v1$\sqrt{\frac{2h}{g}}$ | B. | (v1+v2)$\sqrt{\frac{2h}{g}}$ | ||
| C. | $\sqrt{{h}^{2}+\frac{2h}{g}({v}_{1}+{v}_{2})^{2}}$ | D. | $\sqrt{{h}^{2}+\frac{2h}{g}({v}_{1}-{v}_{2})^{2}}$ |
1.2012年3月31日18时27分,我国在西昌卫星发射中心用“长征三号乙”运载火箭,将法国泰雷兹阿莱尼亚宇航公司制造的亚太7号通信卫星成功送入预定轨道.亚太7号卫星将接替在轨运行的亚太2R卫星,定点于东经76.5°赤道上空,可为亚洲、中东、非洲、澳大利亚、欧洲等提供电视传输和卫星通信服务,并为中国、中东、中亚、非洲等提供电视直播和跨洲际通信广播服务.则下列有关亚太2R卫星与亚太7号通信卫星的说正确的是( )
| A. | 相对于地面静止,轨道半径为确定值 | |
| B. | 亚太2R卫星被替代后,如果要想返回地球必须对其进行加速 | |
| C. | 角速度小于静止在地球赤道上物体的角速度 | |
| D. | 向心加速度大于静止在地球赤道上物体的向心加速度 |
18.1905年,爱因斯坦提出了狭义相对论,关于狭义相对论,下列说法正确的是( )
| A. | 在接近光速运动的火车上时间过得快 | |
| B. | 以接近光速运动的火车,沿运动方向的长度变短 | |
| C. | 所有的物理规律在不同的惯性系中有不同的形式 | |
| D. | 两列以光速相向运动的火车,甲车看乙车的速度是2c |
15.下列相互作用系统的物体,可视为机械能守恒的是( )
| A. | 秋日,离开树树随风飘落的树叶 | |
| B. | 在拉力作用下沿斜面匀速向上运动的物块 | |
| C. | 体育课上,某同学抛出后在空中运动的铅球 | |
| D. | 在黏性较大的液体中由静止释放后下落的小球 |

