题目内容
13. 在许多建筑工地经常使用打夯机将桩料打入泥土中以加固地基.打夯前先将桩料扶起、使其缓慢直立进入泥土中,每次卷扬机都通过滑轮用轻质钢丝绳将夯锤提升到距离桩顶h0=5m处再释放,让夯锤自由下落,若夯锤砸在桩料上并不弹起,并随桩料一起以夯锤砸在桩料前速度的$\frac{1}{2}$向下运动.设夯锤和桩料的质量均为m=500kg,泥土对桩料的阻力为f=kh,其中常数k=2.0×104N/m,h是桩料深入泥土的深度.卷扬机使用电动机来驱动,卷扬机和电动机总的工作效率为η=95%,每次卷扬机需用20s的时间提升夯锤.提升夯锤时忽略加速和减速的过程,不计夯锤提升时的动能,也不计滑轮的摩擦.夯锤和桩料的作用时间极短,g取10m/s2,求:
在许多建筑工地经常使用打夯机将桩料打入泥土中以加固地基.打夯前先将桩料扶起、使其缓慢直立进入泥土中,每次卷扬机都通过滑轮用轻质钢丝绳将夯锤提升到距离桩顶h0=5m处再释放,让夯锤自由下落,若夯锤砸在桩料上并不弹起,并随桩料一起以夯锤砸在桩料前速度的$\frac{1}{2}$向下运动.设夯锤和桩料的质量均为m=500kg,泥土对桩料的阻力为f=kh,其中常数k=2.0×104N/m,h是桩料深入泥土的深度.卷扬机使用电动机来驱动,卷扬机和电动机总的工作效率为η=95%,每次卷扬机需用20s的时间提升夯锤.提升夯锤时忽略加速和减速的过程,不计夯锤提升时的动能,也不计滑轮的摩擦.夯锤和桩料的作用时间极短,g取10m/s2,求:(1)在提升夯锤的过程中,电动机的输入功率.(结果保留2位有效数字)
(2)打完第一夯后,桩料进入泥土的深度.
分析 由能量守恒定律来算出电动机的输入功率;先算出依靠自重桩料可下沉高度,再用平均力做功算出突入泥土的深度.
解答 解:(1)提升夯锤的过程中需做功W=mgh0,
所以W=500×10×5J=2.5×104J.
则卷扬机的输入功率为
P=$\frac{W}{ηt}=\frac{25000}{0.95×20}W=\frac{5}{38}×1{0}^{4}W$=1.3×103W.
(2)依靠自重桩料可下沉h1,有mg=2.0×104h1
所以h1=0.25m,
夯在打击前的速度为v=$\sqrt{2g{h}_{0}}=\sqrt{2×10×5}m/s=10m/s$,
夯锤砸在桩料上的过程时间短,近似看做动量守恒,在竖直方向上,由于夯锤砸在桩料上并不弹起,而随桩料一起向下运动,所以得:
mv=(m+m)v1
打击后的共同速度为v1=5m/s,
下冲过程的阻力是随距离均匀变化的力,可用平均力求做功,下冲过程用动能定理
$0-\frac{1}{2}m{{v}_{1}}^{2}=2mg△h-\frac{1}{2}k[{h}_{1}+({h}_{1}+△h)]△h$,
所以2△h2-△h-2.5=0,$△h=\frac{1+\sqrt{21}}{4}m=1.4m$,
则第一夯打击后桩料深入泥土的浓度为h=h1+△h=1.65m.
答:(1)电动机的输入功率为1.3×103W.
(2)打完第一夯后,桩料进入泥土的深度为1.65m.
点评 本题考查动能定理和能量守恒的使用,难点在于当力随距离均匀变化时,可用平均力求功,也可用图象法,力与距离所夹面积表示功.

练习册系列答案
相关题目
3.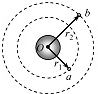 如图,若两颗人造卫星a和b均绕地球做匀速圆周运动,a、b到地心O的距离分别为r1、r2,线速度大小分别为v1、v2,则( )
如图,若两颗人造卫星a和b均绕地球做匀速圆周运动,a、b到地心O的距离分别为r1、r2,线速度大小分别为v1、v2,则( )
 如图,若两颗人造卫星a和b均绕地球做匀速圆周运动,a、b到地心O的距离分别为r1、r2,线速度大小分别为v1、v2,则( )
如图,若两颗人造卫星a和b均绕地球做匀速圆周运动,a、b到地心O的距离分别为r1、r2,线速度大小分别为v1、v2,则( )| A. | $\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{r}_{2}}{{r}_{1}}}$ | B. | $\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{r}_{1}}{{r}_{2}}}$ | C. | $\frac{{v}_{1}}{{v}_{2}}$=($\frac{{r}_{2}}{{r}_{1}}$)2 | D. | $\frac{{v}_{1}}{{v}_{2}}$=($\frac{{r}_{1}}{{r}_{2}}$)2 |
1.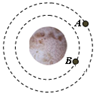 天宫一号由较高的测试轨道,下降到较低的对接轨道,并成功与神舟十号交会对接.如图所示,把两轨道视为圆轨道,下列说法中正确的是( )
天宫一号由较高的测试轨道,下降到较低的对接轨道,并成功与神舟十号交会对接.如图所示,把两轨道视为圆轨道,下列说法中正确的是( )
 天宫一号由较高的测试轨道,下降到较低的对接轨道,并成功与神舟十号交会对接.如图所示,把两轨道视为圆轨道,下列说法中正确的是( )
天宫一号由较高的测试轨道,下降到较低的对接轨道,并成功与神舟十号交会对接.如图所示,把两轨道视为圆轨道,下列说法中正确的是( )| A. | 天宫一号在测试轨道的运动速度大于第一宇宙速度 | |
| B. | 天宫一号在测试轨道比在对接轨道的周期大 | |
| C. | 天宫一号在测试轨道比在对接轨道的加速度大 | |
| D. | 天宫一号在测试轨道比在对接轨道的角速度大 |
8.一定质量的理想气体的压强、内能的变化与气体体积和温度的关系是( )
| A. | 如果保持其体积不变,温度升高,则气体的压强增大,内能增大 | |
| B. | 如果保持其体积不变,温度升高,则气体的压强增大,内能减少 | |
| C. | 如果保持其温度不变,体积增大,则气体的压强减小,内能增大 | |
| D. | 如果保持其温度不变,体积增大,则气体的压强减小,内能不变 |
18.在如图所示的电路中,有一理想的降压变压器,其匝数比为3:1,一额定功率为6W、9V的灯泡L1与变压器的原线圈串接,在变压器的副线圈两端并联接入三个与L1完全相同的灯泡L2、L3、L4,两个理想的交流电表按如图的方式接入电路,已知理想变压器原线圈两端的电压随时间变化的规律如图所示,则下列正确的是( )
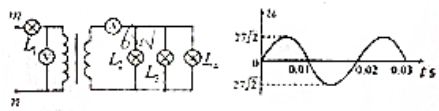

| A. | mn两点间的所加电压的瞬时值为Uab=27$\sqrt{2}$sin100πt(V) | |
| B. | L1、L2、L3、L4均正常发光 | |
| C. | 只有L2、L3、L4正常发光 | |
| D. | 整个电路消耗的总功率为18W |
2. 如图所示.在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(放入小球P后不会改变原来的电场分布).在以后的一段时间内.P在CD连线上做往复运动.下列说法正确的是( )
如图所示.在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(放入小球P后不会改变原来的电场分布).在以后的一段时间内.P在CD连线上做往复运动.下列说法正确的是( )
 如图所示.在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(放入小球P后不会改变原来的电场分布).在以后的一段时间内.P在CD连线上做往复运动.下列说法正确的是( )
如图所示.在光滑绝缘水平面上,两个带等量正电的点电荷M、N,分别固定在A、B两点,O为AB连线的中点,CD为AB的垂直平分线.在CO之间的F点由静止释放一个带负电的小球P(放入小球P后不会改变原来的电场分布).在以后的一段时间内.P在CD连线上做往复运动.下列说法正确的是( )| A. | 小球P的带电量缓慢减小,则它往复运动过程中振幅不断减小 | |
| B. | 小球P的带电量缓慢减小.则它往复运动过程中每次经过O点时的速率不断减小 | |
| C. | 点电荷M,N的电量同时等量地缓慢增大,则小球p往复运动过程中周期不断减小 | |
| D. | 点电荷M,N的带电量同时等量地缓慢增大,则小球p往复运动过程中振幅不断减小 |
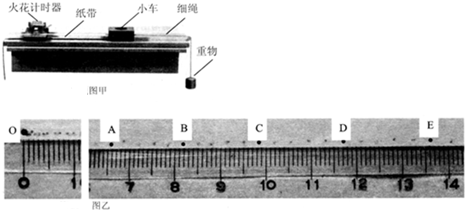
 如图是过山车的部分模型图.模型图中光滑圆形轨道的半径R=8.1m,该光滑圆形轨道固定在倾角为α=37°斜轨道面上的Q点,圆形轨道的最高点A与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使小车(视作质点)从P点以一定的初速度沿斜面向下运动,已知斜轨道面与小车间的动摩擦因数为μ=$\frac{10}{81}$,不计空气阻力,过山车质量为20kg,取g=10m/s2,sin37°=0.6,cos37°=0.8.若小车恰好能通过圆形轨道的最高点A处,求:
如图是过山车的部分模型图.模型图中光滑圆形轨道的半径R=8.1m,该光滑圆形轨道固定在倾角为α=37°斜轨道面上的Q点,圆形轨道的最高点A与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使小车(视作质点)从P点以一定的初速度沿斜面向下运动,已知斜轨道面与小车间的动摩擦因数为μ=$\frac{10}{81}$,不计空气阻力,过山车质量为20kg,取g=10m/s2,sin37°=0.6,cos37°=0.8.若小车恰好能通过圆形轨道的最高点A处,求: