Question

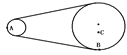
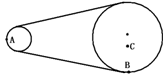
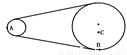
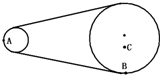
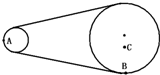在皮带轮传动装置中，已知大轮的半径是小轮半径的3倍，A和B两点分别在两轮的边缘上，C点离大轮轴距离等于小轮半径，若皮带不打滑，则角速度之比ω_A：ω_B：ω_C=

 

，线速度之比v_A：v_B：v_C=

 

，向心加速度之比a_A：a_B：a_C=

 

．

Answer 1

分析：皮带不打滑，A和B两点线速度大小相等，由公式v=ωr，角速度与半径成反比，求出ω_A：ω_B，由公式a_n=

v2

r

研究A、B的向心加速度关系；B、C在同一轮上，角速度相同，由公式v=ωr求解线速度之比，由公式a_n=ω²r研究B、C的向心加速度的关系．

解答：解：①对于A、B两点，皮带不打滑，A和B两点线速度大小相等；
由公式v=ωr，得到：
ω_A：ω_B=r_B：r_A=3：1．
由公式a_n=

v2

r

得到：
a_A：a_B=r_B：r_A=3：1．
②对于B、C两点，B、C在同一轮上，角速度ω相同；
由公式v=ωr得到线速度之比：
v_B：v_C=r_B：r_C=3：1；
由公式a_n=ω²r，得到：
a_B：a_C=r_B：r_C=3：1；
综上得到：
v_A：v_B：v_C=3：3：1
ω_A：ω_B：ω_C=3：1：1；
a_A：a_B：a_C=9：3：1；
故答案为：3：1：1；3：3：1；9：3：1．

点评：本题是圆周运动中典型问题，关键抓住相等量：皮带不打滑时，两轮边缘上各点的线速度大小相等；同一轮上各点的角速度相同．