题目内容
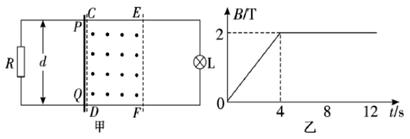
如图所示,足够长的U型光滑导体框架的两个平行导轨间距为L,导轨间连有定值电阻R,框架平面与水平面之间的夹角为θ,不计导体框架的电阻.整个装置处于匀强磁场中,磁场方向垂直于框架平面向上,磁感应强度大小为B 。导体棒ab的质量为m,电阻不计,垂直放在导轨上并由静止释放,重力加速度为g.求:
(1)导体棒ab下滑的最大速度;
(2)导体棒ab以最大速度下滑时定值电阻消耗的电功率。
(1)vm=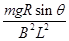 ;(2)P=
;(2)P= 。
。
解析试题分析:(1)当导体棒下滑时,受力平衡,则它下滑的速度最大;
设最大速度为vm,
则导体棒在斜面方向共受到二个力的作用,重力沿斜面的分力,安培力;
故它们存在二力平衡的关系:mgsinθ=BIL,而电流I=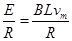 ,
,
代入上式得得vm=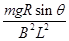 。
。
(2)定值电阻消耗的电功率就是安培力做功的功率大小,
故P=F安·vm=mgsinθ·vm=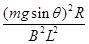 ;
;
也可以通过电流求电功率:
P=I2R=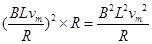 =
=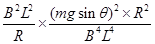 =
=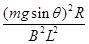 。
。
考点:平衡力,安培力,感应电动势,电功率的简单计算。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
如图,理想变压器原副线圈匝数之比为20: 1,原线圈接入一电压为 u=U0sinωt的交流电源,副线圈接一个R=5.5Ω的负载电阻。若 U0=220 V ,ω=100πrad/s,则下述结论正确的是 ( )
V ,ω=100πrad/s,则下述结论正确的是 ( )
A.副线圈中电压表的读数为 11 V V |
| B.副线圈中输出交流电的周期为0.02s |
| C.原线圈中电流表的读数为0.1A |
| D.原线圈中的输入功率为11W |
 、
、 为间距
为间距 =0.5m足够长的粗糙平行导轨,
=0.5m足够长的粗糙平行导轨, ⊥
⊥ =37°,
=37°, 的电阻。有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为
的电阻。有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为 .将一根质量为
.将一根质量为 =0.05kg、内阻为
=0.05kg、内阻为 的金属棒
的金属棒 紧靠
紧靠 处时刚好达到稳定速度,已知在此过程中通过金属棒截面的电量
处时刚好达到稳定速度,已知在此过程中通过金属棒截面的电量 =0.2C,且金属棒的加速度
=0.2C,且金属棒的加速度 与速度
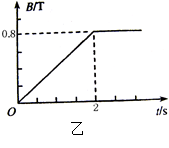
与速度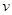 的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与
的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与 =10m/s2,sin37°=0.6,cos37°=0.8)。求:
=10m/s2,sin37°=0.6,cos37°=0.8)。求: 
 上产生的热量。
上产生的热量。 ,回路电阻恒为R,若同时无初速释放两导杆,发现cd沿右导轨下滑
,回路电阻恒为R,若同时无初速释放两导杆,发现cd沿右导轨下滑 距离时,ab杆才开始运动。(认为最大静摩擦力等于滑动摩擦力)。
距离时,ab杆才开始运动。(认为最大静摩擦力等于滑动摩擦力)。