题目内容
照图甲连接电路.电源用直流8V左右,电容器可选几十微法的电解电容器.先使开关S与1端相连,电源向电容器充电,然后把开关S掷向2端,电容器通过电阻R放电,传感器将电流信息传入计算机,屏幕上显示出电流随时间变化的I-t曲线.一位同学测得I-t图象如图乙所示,他的电源电压时8V.
(1)在图中画出一个竖立的狭长矩形(在图乙最左边),它的面积的物理意义是什么?
(2)根据图乙估算电容器在全部放电过程中释放的电荷量Q=
(3)根据以上数据估算的电容是多少C=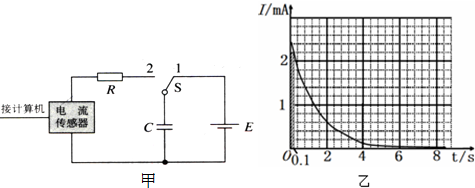
(1)在图中画出一个竖立的狭长矩形(在图乙最左边),它的面积的物理意义是什么?
电容器在此0.1s内所放电荷量
电容器在此0.1s内所放电荷量
(2)根据图乙估算电容器在全部放电过程中释放的电荷量Q=
3.62×10-3~3.68×10-3
3.62×10-3~3.68×10-3
C(3)根据以上数据估算的电容是多少C=
4.4×10-4~4.6×10-4
4.4×10-4~4.6×10-4
F 
分析:(1)由图象的含义可知,横轴与纵轴的乘积即为电量,即可求解;
(2)通过横轴与纵轴的数据,求出一个格子对应的电量,再结合图象所包含的面积,算出多少个格子,从而即可求解;
(3)根据电容器的电容C=
可知,结合电量与电势差,即可求解.
(2)通过横轴与纵轴的数据,求出一个格子对应的电量,再结合图象所包含的面积,算出多少个格子,从而即可求解;
(3)根据电容器的电容C=
| Q |
| U |
解答:解:(1)根据图象的含义,因Q=It,所以竖直狭长矩形的面积表示为:在0.1s内电容器的放电量;
(2)根据横轴与纵轴的数据可知,一个格子的电量为0.08×10-3C,由大于半格算一个,小于半格舍去,因此图象所包含的格子个数为45,
所以释放的电荷量是q=0.08×10-3C×45=3.6×10-3C;
(3)根据电容器的电容C=
可知,C=
F=4.5×10-4F;
故答案为:(1)电容器在此0.1s内所放电荷量
(2)3.62×10-3~3.68×10-3 C
(3)4.4×10-4~4.6×10-4 F
(2)根据横轴与纵轴的数据可知,一个格子的电量为0.08×10-3C,由大于半格算一个,小于半格舍去,因此图象所包含的格子个数为45,
所以释放的电荷量是q=0.08×10-3C×45=3.6×10-3C;
(3)根据电容器的电容C=
| Q |
| U |
| 3.6×10-3 |
| 8 |
故答案为:(1)电容器在此0.1s内所放电荷量
(2)3.62×10-3~3.68×10-3 C
(3)4.4×10-4~4.6×10-4 F
点评:考查图象的含义,知道如何通过图象求电量,掌握电容器的电容公式,理解其比值定义法.

练习册系列答案
相关题目



 和内阻
和内阻 .
. 可以从刻度盘上直接读出,
可以从刻度盘上直接读出,  为待测电流表,R为电位器,R/为电阻箱,E为电源,S为开关;试在右侧所给的器材实物图中选择合适的器材连接成测量电路.
为待测电流表,R为电位器,R/为电阻箱,E为电源,S为开关;试在右侧所给的器材实物图中选择合适的器材连接成测量电路.
 ,此时电阻箱的电阻为R0该同学能否据此测出电流表内阻
(填能或不能);若能,该电流表的内阻为多少
,此时电阻箱的电阻为R0该同学能否据此测出电流表内阻
(填能或不能);若能,该电流表的内阻为多少