题目内容
2.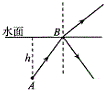 如图所示,一个足够大的水池盛满清水,水深h=4m,水池底部中心有一点光源A,其中一条光线斜射到水面上距A为l=5m的B点时,它的反射光线与折射光线恰好垂直.
如图所示,一个足够大的水池盛满清水,水深h=4m,水池底部中心有一点光源A,其中一条光线斜射到水面上距A为l=5m的B点时,它的反射光线与折射光线恰好垂直.(1)求水的折射率n;
(2)用折射率n和水深h表示水面上被光源照亮部分的面积(圆周率用π表示).
分析 (1)由几何关系求出入射角,结合反射光线与折射光线恰好垂直,求出折射角,再根据折射定律求解水的折射率;
(2)当光恰好发生全反射,亮斑面积最大,由sinC=$\frac{1}{n}$可求出临界角,再由几何关系,可求出水面上被光源照亮部分的面积.
解答 解:(ⅰ)设射向B点的光线入射角与折射角分别i和r,
由题意得 sini=$\frac{\sqrt{{l}^{2}-{h}^{2}}}{l}$=$\frac{\sqrt{{5}^{2}-{4}^{2}}}{5}$=0.6,i=37°
i+r=90°
则 r=53°
故水的折射率为 n=$\frac{sinr}{sini}$=$\frac{sin53°}{sin37°}$=$\frac{4}{3}$≈1.33
(ⅱ)设射向水面的光发生全反射的临界角为C
则有 sinC=$\frac{1}{n}$
圆形光斑的半径为 R=htanC
圆形光斑的面积为 S=πR2
联立可解得 S=$\frac{π{h}^{2}}{{n}^{2}-1}$
答:
(1)水的折射率n为1.33;
(2)水面上被光源照亮部分的面积为$\frac{π{h}^{2}}{{n}^{2}-1}$.
点评 本题考查光的折射定律与光的全反射现象,运用几何知识来解题,同时注意全反射的条件.

练习册系列答案
相关题目
1.在方向垂直纸面向里的匀强磁场中,一个静止的${\;}_{92}^{238}$U发生α衰变后,生成一个钍核.若衰变后钍核和α粒子的运动方向都与磁场方向垂直,钍核和α粒子均不计重力,则( )
| A. | 该衰变方程为${\;}_{92}^{238}$U→${\;}_{2}^{4}$He+${\;}_{90}^{234}$Th | |
| B. | 钍核与α粒子作匀速圆周运动的轨迹圆相内切 | |
| C. | 钍核的动能比α粒子的动能大 | |
| D. | 从钍核与α粒子分离到两者再次相遇,α粒子绕圆心转过的角度比钍核多6π |
10.下列说法正确的是( )
| A. | 汤姆孙发现电子,提出原子的核式结构模型 | |
| B. | 金属的逸出功随入射光的频率增大而增大 | |
| C. | 核力存在于原子核内所有核子之间 | |
| D. | 核电站是利用重核裂变反应所释放的核能转化为电能 |
17.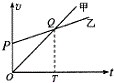 甲、乙两车在一平直道路上同向运动,其v-t图象如图所示,图中△OPQ和△OQT的面积分别为S1和S2(S2>S1),计时开始时,甲、乙两车相距S0,在两车运动过程中,下列说法正确的是( )
甲、乙两车在一平直道路上同向运动,其v-t图象如图所示,图中△OPQ和△OQT的面积分别为S1和S2(S2>S1),计时开始时,甲、乙两车相距S0,在两车运动过程中,下列说法正确的是( )
 甲、乙两车在一平直道路上同向运动,其v-t图象如图所示,图中△OPQ和△OQT的面积分别为S1和S2(S2>S1),计时开始时,甲、乙两车相距S0,在两车运动过程中,下列说法正确的是( )
甲、乙两车在一平直道路上同向运动,其v-t图象如图所示,图中△OPQ和△OQT的面积分别为S1和S2(S2>S1),计时开始时,甲、乙两车相距S0,在两车运动过程中,下列说法正确的是( )| A. | 若甲车在乙车前方且S0=S1+S2,两车相遇1次 | |
| B. | 若甲车在乙车前方且S0<S1,两车相遇2次 | |
| C. | 若乙车在甲车前方且S0=S2,两车不会相遇 | |
| D. | 若乙车在甲车前方且S0=S1,甲车追上乙前T时刻相距最近 |
11.下列数据最接近实际情况的是( )
| A. | 使人感到舒适的温度约是23℃ | |
| B. | 台灯正常工作时的电流约是2A | |
| C. | 中学生步行的速度约是5m/s | |
| D. | 中学生从一楼匀速上到三楼所做的功约是300J |
12.关于原子和原子核,下列说法正确的是( )
| A. | α粒子散射实验揭示了原子核内部的复杂性 | |
| B. | 光电效应实验揭示了光的粒子性 | |
| C. | 核反应方程中,质量和电荷是守恒的 | |
| D. | 根据玻尔理论可知,一群氢原子核外电子从n=4能级向低能级跃迁最多可辐射6种频率的光子 |
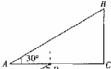 如图所示,一截面为直角三角形的玻璃棱镜ABC,∠A=30°.一条光线以60°的入射角从AC边上的D点射入棱镜,光线垂直BC射出棱镜.已知A、D间距为L,求:
如图所示,一截面为直角三角形的玻璃棱镜ABC,∠A=30°.一条光线以60°的入射角从AC边上的D点射入棱镜,光线垂直BC射出棱镜.已知A、D间距为L,求: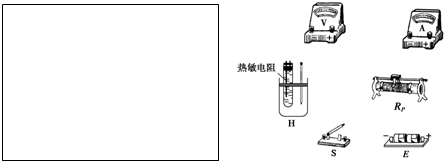
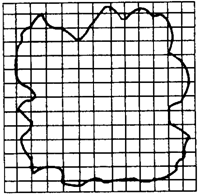 在课本上粗测油酸分子的大小的实验中,油酸酒精溶液的浓度为每104mL溶液中有纯油酸6mL,用注射器量得1mL上述溶液有75滴,把一滴该溶液滴入盛水的表面撒有痱子粉的浅盘里,待水面稳定后,测得油酸膜的近似轮廓如图所示,图中正方形小方格的边长为1cm.则
在课本上粗测油酸分子的大小的实验中,油酸酒精溶液的浓度为每104mL溶液中有纯油酸6mL,用注射器量得1mL上述溶液有75滴,把一滴该溶液滴入盛水的表面撒有痱子粉的浅盘里,待水面稳定后,测得油酸膜的近似轮廓如图所示,图中正方形小方格的边长为1cm.则