题目内容
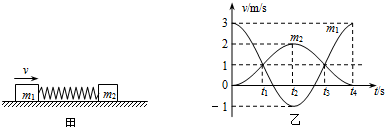
如图甲所示,一轻弹簧的两端与质量分别为mA和mB的两物块A、B相连接,并静止在光滑的水平面上,已知mA=1 kg.现使A瞬时获得水平向右的初速度v0,从此时刻开始计时,两物块的速度随时间变化的规律如图乙所示,其中A物块的速度图线略去了开始的一小段.已知弹簧始终处于弹性限度内.试求:
(1)物块A的初速度v0的大小和物块B的质量mB;
(2)在A、B和弹簧相互作用的过程中,弹簧的最大弹性势能.
解:(1)由乙图可知,t1时刻A、B速度相同且为v=1 m/s;t2时刻,弹簧处于自由状态,
vA=-1 m/s,vB=2 m/s.
由动量守恒定律和能量守恒定律得mAv0=(mA+mB)v ①
![]() mAv02=
mAv02=![]() mA vA 2+
mA vA 2+![]() mBvB2 ②
mBvB2 ②
代入数据求得v0=3 m/s ③
mB=2 kg ④
(2)当两物块速度相同时,弹簧的弹性势能最大为Em,根据能量守恒定律得
Em=![]() mAv02-
mAv02-![]() (mA+mB)v2=3 J ⑤
(mA+mB)v2=3 J ⑤

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图甲所示,一轻弹簧的两端与质量分别为m1和m2的两物块A?B相连接,并静止在光滑的水平面上.现使A瞬时获得水平向右的速度3 m/s,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示,从图象信息可得( )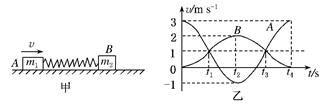
| A.在t1?t3时刻两物块达到共同速度1m/s,且弹簧都是处于压缩状态 |
| B.从t3到t4时刻弹簧由压缩状态恢复到原长 |
| C.两物体的质量之比为m1:m2=1:2 |
| D.在t2时刻A与B的动能之比为Ek1:Ek2=1:8 |