题目内容
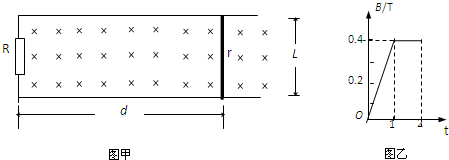
如图甲所示，在水平面上固定有宽为L=1.0m足够长的金属平行导轨，导轨左端接有的R=0.5Ω的电阻，垂直于导轨平面有一磁场，且磁感应强度随时间变化规律如图乙所示．在t=0时刻，在距导轨左端d=5m处有一阻值r=0.5Ω光滑导体棒，放置在导轨上，第1S内导体棒在一变力作用下始终处于静止状态，不计导体棒与导轨之间的接触电阻．求
（1）第1s内的感应电动势大小；
（2）第1s末拉力的大小及方向；
（3）若1s后拉力保持与第1s末相同，求导体棒的最终速度．
（1）第1s内的感应电动势大小；
（2）第1s末拉力的大小及方向；
（3）若1s后拉力保持与第1s末相同，求导体棒的最终速度．
（1）第1s内由电磁感应定律可得：
电动势为E=
=Ld
=2V．
（2）由闭合电路欧姆定律知I=
=2A
F安=BIL=0.8N
由平衡条件知F=F安=0.8N
由楞次定律可得，感应电流的方向为逆时针方向，根据左手定则，导体棒安培力的方向水平向左，则拉力方向水平向右．
（3）1s后导体棒做变加速直线运动，当受力平衡速度达最大
则由电磁感应定律E′=BLv
由闭合电路欧姆定律知I′=
．
由平衡条件知F′=F安′=I′LB
联立解得v=
代入数据得V=5m/s．
答：（1）第1s内的感应电动势大小为2V．
（2）第1s末拉力的大小为0.8N，方向水平向右．
（3）导体棒的最终速度为5m/s．
电动势为E=
| △Φ |
| △t |
| △B |
| △t |
（2）由闭合电路欧姆定律知I=
| E |
| R+r |
F安=BIL=0.8N
由平衡条件知F=F安=0.8N
由楞次定律可得，感应电流的方向为逆时针方向，根据左手定则，导体棒安培力的方向水平向左，则拉力方向水平向右．
（3）1s后导体棒做变加速直线运动，当受力平衡速度达最大
则由电磁感应定律E′=BLv
由闭合电路欧姆定律知I′=
| E′ |
| R+r |
由平衡条件知F′=F安′=I′LB
联立解得v=
| F′(R+r) |
| B2L2 |
代入数据得V=5m/s．
答：（1）第1s内的感应电动势大小为2V．
（2）第1s末拉力的大小为0.8N，方向水平向右．
（3）导体棒的最终速度为5m/s．
练习册系列答案
相关题目
如图甲所示，在水平面内的三个质点分别位于直角三角形 ABC的顶点上，已知AB=6m，AC=8m．t0=0时刻A、B开始振动，波动图象均如图乙所示，所形成的机械波在水平面内传播，在t=4s时C点开始振动．则
如图甲所示，在水平面内的三个质点分别位于直角三角形ABC的顶点上，已知AB=6m，AC=8m．t0=0时刻A、B开始振动，振动图象均如图乙所示．所形成的机械波在水平面内传播，在t=4s时C点开始振动．则该机械波的传播速度大小为
如图甲所示，在水平面内的三个质点分别位于直角三角形ABC的顶点上，已知AB=6m，AC=8m．t0=0时刻A、B开始振动，波动图象均如图乙所示，所形成的机械波在水平面内传播，在t=4s时C点开始振动．则 （ ）
如图甲所示，在水平面内的三个质点分别位于直角三角形ABC的顶点上，已知AB=6m，AC=8m．t0=0时刻A、B开始振动，波动图象均如图乙所示，所形成的机械波在水平面内传播，在t=4s时C点开始振动．则（ ）| A、该机械波的传播速度大小为4m/s | B、两列波相遇后，C点振动加强 | C、该两列波的波长是2m | D、该两列波的周期T=1s |