题目内容
A、B两列火车,在同一轨道上同向行驶,A车在前,其速度vA=10m/s,B车在后,速度vB=30m/s.因大雾能见度很低,B车在距A车△s=75m时才发现前方有A车,这时B车立即刹车,但B车要经过180m才能够停止.问:
(1)B车刹车后的加速度是多大?
(2)若B车刹车时A车仍按原速前进,请判断两车是否相撞?若会相撞,将在B车刹车后何时?若不会相撞,则两车最近距离是多少?
(3)若B车在刹车的同时发出信号,A车司机经过△t=4s收到信号后加速前进,则A车的加速度至少多大才能避免相撞?
解:(1)B车刹车至停下过程中,vt=0,v0=vA=30m/s,S=180m
由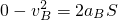 ,解得:
,解得: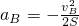 =
=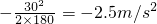
故B车刹车时加速度大小为2.5m/s2,方向与运动方向相反.
(2)假设始终不相撞,设经时间t两车速度相等,则对B车有:vA=vB+aBt,解得: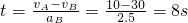
此时B车的位移:
A车的位移:SA=vAt=10×8=80m
因SB=160m>△S+SA=155m,故两车会相撞.
设经时间t两车相撞,则有: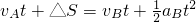
代入数据解得:t1=6s,t2=10s
故经时间6s两车相撞.
(3)设A车的加速度为aA时两车不相撞:
两车速度相等时:vB+aBt'=vA+aA(t'-△t),
即:30-2.5t'=10+aA(t'-△t)
此时B车的位移: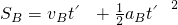 ,即:
,即: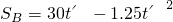
A车的位移: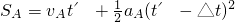
要不相撞,两车位移关系满足:SB≤SA+△S
由以上解得: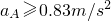
答:(1)B车刹车后的加速度是-2.5m/s2;
(2)若B车刹车时A车仍按原速前进,两车相撞;将在B车刹车后6s相遇;
(3)若B车在刹车的同时发出信号,A车司机经过△t=4s收到信号后加速前进,则A车的加速度至少达到0.83m/s2才能避免相撞.
分析:(1)根据速度位移关系公式列式求解;
(2)当速度相同时,求解出各自的位移后结合空间距离分析;或者以前车为参考系分析;
(3)两车恰好不相撞的临界条件是两部车相遇时速度相同,根据运动学公式列式后联立求解即可.
点评:本题第二问关键要判断能否追上,注意运动学公式的适用范围;第三问关键是找到恰好不追上的临界条件,较难.
由
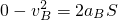 ,解得:
,解得: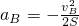 =
=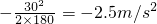
故B车刹车时加速度大小为2.5m/s2,方向与运动方向相反.
(2)假设始终不相撞,设经时间t两车速度相等,则对B车有:vA=vB+aBt,解得:
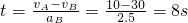
此时B车的位移:

A车的位移:SA=vAt=10×8=80m
因SB=160m>△S+SA=155m,故两车会相撞.
设经时间t两车相撞,则有:
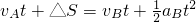
代入数据解得:t1=6s,t2=10s
故经时间6s两车相撞.
(3)设A车的加速度为aA时两车不相撞:
两车速度相等时:vB+aBt'=vA+aA(t'-△t),
即:30-2.5t'=10+aA(t'-△t)
此时B车的位移:
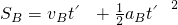 ,即:
,即: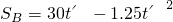
A车的位移:
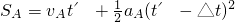
要不相撞,两车位移关系满足:SB≤SA+△S
由以上解得:
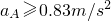
答:(1)B车刹车后的加速度是-2.5m/s2;
(2)若B车刹车时A车仍按原速前进,两车相撞;将在B车刹车后6s相遇;
(3)若B车在刹车的同时发出信号,A车司机经过△t=4s收到信号后加速前进,则A车的加速度至少达到0.83m/s2才能避免相撞.
分析:(1)根据速度位移关系公式列式求解;
(2)当速度相同时,求解出各自的位移后结合空间距离分析;或者以前车为参考系分析;
(3)两车恰好不相撞的临界条件是两部车相遇时速度相同,根据运动学公式列式后联立求解即可.
点评:本题第二问关键要判断能否追上,注意运动学公式的适用范围;第三问关键是找到恰好不追上的临界条件,较难.

练习册系列答案
相关题目
 车在此行驶速度的情况下刹车需要经过1815m才能够停止,试求:
车在此行驶速度的情况下刹车需要经过1815m才能够停止,试求: