题目内容
6.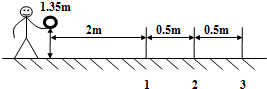 “套圈”是一项老少皆宜的体育运动项目.如图所示,水平地面上固定着3根直杆1、2、3,直杆的粗细不计,高度均为0.1m,相邻两直杆之间的距离为0.5m.比赛时,运动员将内圆直径为0.2m的环沿水平方向抛出,刚抛出时环平面距地面的高度为1.35m,环的中心与直杆1的水平距离为2m.假设直杆与环的中心位于同一竖直面,且运动中环心始终在该平面上,环面在空中保持水平,忽略空气阻力的影响,g取10m/s2.以下说法正确的是( )
“套圈”是一项老少皆宜的体育运动项目.如图所示,水平地面上固定着3根直杆1、2、3,直杆的粗细不计,高度均为0.1m,相邻两直杆之间的距离为0.5m.比赛时,运动员将内圆直径为0.2m的环沿水平方向抛出,刚抛出时环平面距地面的高度为1.35m,环的中心与直杆1的水平距离为2m.假设直杆与环的中心位于同一竖直面,且运动中环心始终在该平面上,环面在空中保持水平,忽略空气阻力的影响,g取10m/s2.以下说法正确的是( )| A. | 如果能够套中直杆,环抛出时的水平初速度不能小于3.9m/s | |
| B. | 如果能够套中第2根直杆,环抛出时的水平初速度范围在4.8m/s到5.2m/s之间 | |
| C. | 如环抛出的水平速度大于6.1m/s,就不能套中第3根直杆 | |
| D. | 如以4m/s的水平初速度将环抛出,就可以套中第1根直杆 |
分析 运动员将环沿水平方向抛出后做平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动,要够套中第一根直杆,竖直方向下落1.25m时,水平方向的位移范围为1.9-2.1m之间,要能套中第2根直杆,水平方向的位移范围为2.4-2.6m之间,要使环套不中第3根直杆,则水平位移要大于3.1m,根据平抛运动的基本规律即可求解.
解答 解:运动员将环沿水平方向抛出后做平抛运动,要够套中直杆,竖直方向下落的位移为1.25m,则
$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×1.25}{10}}=0.5s$
A、如果能够套中直杆,水平方向的位移x≥2-0.1=1.9m,则${v}_{0}^{\;}$=$\frac{x}{t}=\frac{1.9}{o.5}=3.8m/s$,故A错误;
B、要能套中第2根直杆,水平方向的位移范围为2.4-2.6m之间,根据${v}_{0}^{\;}$=$\frac{x}{t}$可得:水平速度的范围为$\frac{2.4}{0.5}m/s≤{v}_{0}^{\;}≤\frac{2.6}{0.5}m/s$,即4.8m/s≤v0≤5.2m/s,故B正确;
C、要使环套不中第3根直杆,则水平位移要大于3.1m,则${v}_{0}^{\;}=\frac{x}{t}=\frac{3.1}{0.5}m/s=6.2m/s$,故C错误.
D、要能套中第1根直杆,水平方向的位移范围为1.9-2.1m之间,根据${v}_{0}^{\;}=\frac{x}{t}$可得:水平速度的范围为$\frac{1.9}{0.5}m/s≤{v}_{0}^{\;}≤\frac{2.1}{0.5}m/s$,即3.8m/s≤v0≤4.2m/s,则如4m/s的水平初速度将环抛出,就可以套中第1根直杆,故D正确;
故选:BD
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道平抛运动的时间由高度决定,初速度和时间共同决定水平位移.

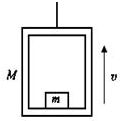 如图所示,质量为M的电梯底板上放置一质量为m的物体,钢索拉着电梯由静止开始向上做加速运动,当上升高度为 H时,速度达到v,不计空气阻力,则( )
如图所示,质量为M的电梯底板上放置一质量为m的物体,钢索拉着电梯由静止开始向上做加速运动,当上升高度为 H时,速度达到v,不计空气阻力,则( )| A. | 物体所受合力做的功等于$\frac{1}{2}$mv2+mgH | |
| B. | 钢索的拉力做的功等于$\frac{1}{2}$mv2+MgH | |
| C. | 此过程中电梯的机械效率为$\frac{m}{(M+m)}$ | |
| D. | 钢索的拉力、电梯的重力及物体对底板的压力对电梯M做的总功等于$\frac{1}{2}$Mv2 |
| A. | 第一宇宙速度是人造地球卫星的最小发射速度,其等于地球赤道上物体的线速度 | |
| B. | 所有地球卫星的发射速度都大于或等于7.9 km/s | |
| C. | 第二宇宙速度是使物体挣脱地球引力束缚的最小发射速度,其大小为11.2 km/s | |
| D. | 第三宇宙速度是使物体挣脱太阳引力束缚的最小发射速度,其大小为16.7 km/s |
| A. | 物块减少的重力势能转化为物块增加的动能和物块与斜面增加的内能 | |
| B. | 物块减少的重力势能等于物块增加的动能和物块与斜面增加的内能之和 | |
| C. | 物块减少的重力势能等于物块增加的动能,能量只是在机械能内部转化 | |
| D. | 能量不会凭空产生,也不会凭空消失,在转化或转移的过程中总量保持不变 |
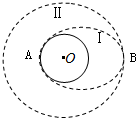 如图所示,在发射某地球卫星的过程中,首先将卫星从A点发射进入椭圆轨道Ⅰ运行,然后在B点通过改变卫星速度,让卫星进入预定圆轨道Ⅱ上运行,则( )
如图所示,在发射某地球卫星的过程中,首先将卫星从A点发射进入椭圆轨道Ⅰ运行,然后在B点通过改变卫星速度,让卫星进入预定圆轨道Ⅱ上运行,则( )| A. | 该卫星的发射速度必定大于7.9km/s | |
| B. | 卫星在椭圆轨道Ⅰ运行的过程中,经过A点的速度小于经过B点的速度 | |
| C. | 卫星在椭圆轨道Ⅰ经过A点的加速度等于在圆轨道Ⅱ经过B点的加速度速度 | |
| D. | 卫星在椭圆轨道Ⅰ经过B点时的机械能小于在圆轨道Ⅱ经过B点时的机械能 |
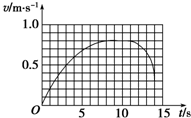 利用速度传感器与计算机结合,可以自动作出物体运动的图象.某同学在一次实验中得到的运动小车的速度-时间图象如图所示,以下说法正确的是( )
利用速度传感器与计算机结合,可以自动作出物体运动的图象.某同学在一次实验中得到的运动小车的速度-时间图象如图所示,以下说法正确的是( )| A. | 小车先做加速运动,然后做减速运动 | |
| B. | 小车运动的最大速度约为0.8 m/s | |
| C. | 小车的位移一定大于8 m | |
| D. | 小车做曲线运动 |
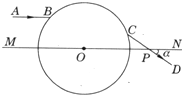 如图所示,一透明球体置于空气中,球半径为R=10Cm,折射率n=$\sqrt{2}$.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,其中B为入射点,AB与MN间距为5$\sqrt{2}$cm,CD为出射光线.
如图所示,一透明球体置于空气中,球半径为R=10Cm,折射率n=$\sqrt{2}$.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,其中B为入射点,AB与MN间距为5$\sqrt{2}$cm,CD为出射光线. 如图,一辆质量为1000kg的汽车静止在一座半径为40m的圆弧形拱桥顶部(取g=10m/s2)
如图,一辆质量为1000kg的汽车静止在一座半径为40m的圆弧形拱桥顶部(取g=10m/s2)