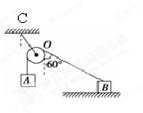
题目内容

如图所示，一质量为M的楔形木块放在水平桌面上，它的顶角为90°，两底角为α和β，a、b为两个位于斜面上质量均为m的小木块。已知所有接触面都是光滑的。现发现a、b沿斜面下滑，而楔形木块静止不动，这时楔形木块对水平桌面的压力等于
A．Mg+2mgB．Mg+mgC．Mg+mg(sinα+sinβ)D．Mg+mg(cosα+cosβ)
B

试题分析：对木块a受力分析，如图，受重力和支持力

由几何关系，得到  N1=mgcosα
故物体a对斜面体的压力为N1′="mgcosα" ①
同理，物体b对斜面体的压力为N2′="mgcosβ" ②
对斜面体受力分析，如图，假设摩擦力向左

根据共点力平衡条件，得到f+N2′cosα-N1′cosβ="0" ③
F支-Mg-N1′sinβ-N2′sinβ="0" ④
根据题意α+β="90°" ⑤
由①～⑤式解得F支=Mg+mg
根据牛顿第三定律，斜面体对地的压力等于Mg+mg，B正确。
练习册系列答案
相关题目
如图所示，物块在力F作用下向右沿水平方向匀速运动，则物块受到的摩擦力Ff与拉力F的合力方向应该是(　　)
A．水平向右B．竖直向上C．向右偏上D．向左偏上
如图所示，质量为m的木块，被水平力F紧压在倾角为θ=60°的墙面上处于静止。则关于木块的受力情况、墙面对木块的作用力（压力与摩擦力的合力），下列说法正确的是（   ）
A．墙面对木块一定有压力
B．墙面对木块一定有摩擦力
C．墙面对木块的作用力为
D．墙面对木块的作用力为
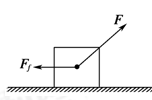
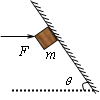
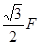
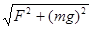
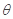如图所示，在高度不同的两水平台阶上放有质量分别为m1、m2的两物体，物体间用轻弹簧相连，弹簧与竖直方向夹角为。在m1左端施加水平拉力F，使m1、m2均处于静止状态，已知m1表面光滑，重力加速度为g，则下列说法正确的是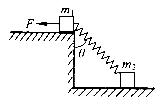
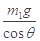
A．弹簧弹力的大小为B．地面对m2的摩擦力大小为F
C．地面对m2的支持力可能为零D．ml与m2一定相等
用L=30cm的细线将质量为4×10-3㎏的带电小球P悬挂在Ｏ点下，当空中有方向为水平向右，大小为1×104N/C的匀强电场时，小球偏转37°后处在静止状态。

（1）分析小球的带电性质；
（2）求小球的带电量；
（3）求细线的拉力。
如图所示，三根细线OA、OB 、OC最大承受力相同。其中OB水平，A端、B端固定。若逐渐增加C端所挂物体质量，则最先断的绳（  ）

A．必定是OA　　                     B．必定是OB　　
C．必定是OC　　                     D．可能是OB，也可能是OC
如图所示，物体A放在直角三角形斜面体B上面，B放在弹簧上面并紧挨着竖直墙壁，初始时A、B静止；现用力F沿斜面向上推A，但A、B仍保持静止。施加推力F后下列说法正确的是

A.A、B之间的摩擦力大小可能不变              B.A、B之间的摩擦力一定变小
C.B与墙之间可能没有摩擦力                   D.弹簧弹力一定变化
用三根轻绳将重量为G的物块悬挂在空中，如图所示，已知ac和bc与竖直方向的夹角分别为30°和60°，则ac绳和bc绳中的拉力分别为（ ）
A．，B．，
C．，D．，
（8分）如图所示，拉B物体的轻绳与竖直方向成60°角，O为一定滑轮，物体A与B之间用跨过定滑轮的细绳相连且均保持静止，已知B的重力为100 N，水平地面对B的支持力为80 N，绳和滑轮的质量以及摩擦均不计，试求：

（1）物体A的重力和物体B与地面间的摩擦力？
（2）连接定滑轮的OC绳所受拉力大小和方向？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网