题目内容
 如图所示,物体质量为m,靠在粗糙的竖直墙上,物体与墙间的动摩擦因数为μ,要使物体沿着墙匀速滑动,则外力F的大小可能是( )
如图所示,物体质量为m,靠在粗糙的竖直墙上,物体与墙间的动摩擦因数为μ,要使物体沿着墙匀速滑动,则外力F的大小可能是( )分析:当物体匀速上滑时,摩擦力沿墙壁向下;当物匀速下滑时,摩擦力沿墙壁向上.根据平衡条件和摩擦力公式并运用正交分解法列式求出F.
解答:解:当物体上滑时,静摩擦力沿墙壁向下此时力F较大,设为F1.物体的受力图如图1.
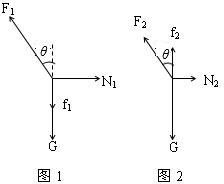
根据正交分解得:
N1=F1sinθ
f1+G=F1cosθ
又f1=μN1,联立解得
F1=
当物体匀速下滑时,摩擦力沿墙壁向,此时力F较小,设为F2,如图2;
根据正交分解得:
N2=F2sinθ
f2+F2cosθ=G
又f2=μN2,联立解得
F2=
故选BD.

根据正交分解得:
N1=F1sinθ
f1+G=F1cosθ
又f1=μN1,联立解得
F1=
| mg |
| cosθ-μsinθ |
当物体匀速下滑时,摩擦力沿墙壁向,此时力F较小,设为F2,如图2;
根据正交分解得:
N2=F2sinθ
f2+F2cosθ=G
又f2=μN2,联立解得
F2=
| mg |
| sinθ+μcosθ |
故选BD.
点评:本题是力平衡问题,关键分析清楚摩擦力的两种可能情况:当物体向上或向下滑动时,物体与墙壁间的摩擦力不同.处理方法可以分情况讨论,也可以假设摩擦力向上,取正负两种值.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
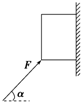 如图所示,物体质量为m,靠在粗糙的竖直墙上,物体与墙之间的动摩擦因数为μ,若要使物体沿着墙向下匀速运动,则外力F的大小为多少?
如图所示,物体质量为m,靠在粗糙的竖直墙上,物体与墙之间的动摩擦因数为μ,若要使物体沿着墙向下匀速运动,则外力F的大小为多少? 如图所示,物体质量为2kg,外力F=50N作用在物体上,F与水平线夹角α=37°,使物体匀速上滑(sin37°=0.6,cos37°=0.8,g=10m/s2)求:物体与墙之间的动摩擦因数是多少?
如图所示,物体质量为2kg,外力F=50N作用在物体上,F与水平线夹角α=37°,使物体匀速上滑(sin37°=0.6,cos37°=0.8,g=10m/s2)求:物体与墙之间的动摩擦因数是多少? 如图所示,物体质量为m,靠在粗糙的竖直墙上,物体与墙间的动摩擦因数为μ.要使物体沿墙匀速滑动,则外力F的大小可能是( )
如图所示,物体质量为m,靠在粗糙的竖直墙上,物体与墙间的动摩擦因数为μ.要使物体沿墙匀速滑动,则外力F的大小可能是( ) 如图所示,物体质量为1kg,一个力F=10N斜向上拉,物体和水平面间的动摩擦因数μ=0.25,物体在F的作用下前进10m,则在这段时间内,摩擦力f对物体做的功是
如图所示,物体质量为1kg,一个力F=10N斜向上拉,物体和水平面间的动摩擦因数μ=0.25,物体在F的作用下前进10m,则在这段时间内,摩擦力f对物体做的功是