题目内容
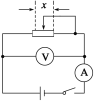
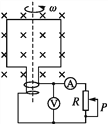
【题目】如图所示，一条带有圆轨道的长轨道水平固定，圆轨道竖直，底端分别与两侧的直轨道相切，半径R＝0.5m，物块A以v0＝6m/s的速度滑入圆轨道，滑过最高点Q，再沿圆轨道滑出后，与直轨道上P处静止的物块B碰撞，碰后粘在一起运动，P点左侧轨道光滑，右侧轨道呈粗糙段、光滑段交替排列，每段长度都为L＝0.1m，物块与各粗糙段间的动摩擦因数都为μ＝0.1，A、B的质量均为m＝1kg(重力加速度g取10m/s2；A、B视为质点，碰撞时间极短)．
(1)求A滑过Q点时的速度大小v和受到的弹力大小F；
(2)若碰后AB最终停止在第k个粗糙段上，求k的数值；
(3)求碰后AB滑至第n个(n＜k)光滑段上的速度vn与n的关系式．
【答案】(1)
, F＝22 N (2) k＝45 (3)
【解析】
⑴物块A从开始运动到运动至Q点的过程中，受重力和轨道的弹力作用，但弹力始终不做功，只有重力做功，根据动能定理有：－2mgR＝
－
解得：v＝
＝4m/s
在Q点，不妨假设轨道对物块A的弹力F方向竖直向下，根据向心力公式有：mg＋F＝
解得：F＝－mg＝22N，为正值，说明方向与假设方向相同。
⑵根据机械能守恒定律可知，物块A与物块B碰撞前瞬间的速度为v0，设碰后A、B瞬间一起运动的速度为v0′，根据动量守恒定律有：mv0＝2mv0′
解得：v0′＝
＝3m/s
设物块A与物块B整体在粗糙段上滑行的总路程为s，根据动能定理有：－2μmgs＝0－
解得：s＝
＝4.5m
所以物块A与物块B整体在粗糙段上滑行的总路程为每段粗糙直轨道长度的
＝45倍，即k＝45
⑶物块A与物块B整体在每段粗糙直轨道上做匀减速直线运动，根据牛顿第二定律可知，其加速度为：a＝
＝－μg＝－1m/s2
由题意可知AB滑至第n个（n＜k）光滑段时，先前已经滑过n个粗糙段，根据匀变速直线运动速度-位移关系式有：2naL＝
－
解得：vn＝
＝
m/s（其中n＝1、2、3、…、44）
