题目内容
在科学研究中,可以通过施加适当的电场和磁场来实现对带电粒子运动的控制. 如图1所示的xOy平面处于匀强电场和匀强磁场中,电场强度E和磁感应强度B随时间t作周期性变化的图象如图2所示.x轴正方向为E的正方向,垂直纸面向里为B的正方向.在坐标原点O有一粒子P,其质量和电荷量分别为m和+q.不计重力. 在t=τ/2时刻释放P,它恰能沿一定轨道做往复运动.

(1)求P在磁场中运动时速度的大小v0;
(2)求B0应满足的关系;
(3)在t0(0<t0<τ/2)时刻释放P,求P速度为零时的坐标.

(1)求P在磁场中运动时速度的大小v0;
(2)求B0应满足的关系;
(3)在t0(0<t0<τ/2)时刻释放P,求P速度为零时的坐标.
分析:(1)在t=
τ时刻释放带电粒子P,在
τ~τ时间内做匀加速直线运动,τ~2τ时间内做匀速圆周运动,根据牛顿第二定律和运动学公式结合求出v0;
(2)由题,粒子恰能沿一定轨道做往复运动,分析可知,当t=2τ时刻,P在磁场中作圆周运动结束后并开始沿x轴负方向运动,才能沿一定的轨道作往复运动,画出轨迹,确定出粒子在磁场中圆周运动的周期,粒子在磁场中由洛伦兹力提供向心力,由牛顿第二定律和圆周运动的运动学公式求解B0应满足的关系;
(3)在t0(0<t0<τ/2)时刻释放P,P在电场中加速时间为τ-t0,由上题结果得到粒子在磁场中圆周运动的速度和半径,粒子又经过(τ-t0)时间速度减至零后向右加速时间为t0,根据几何知识求解P速度为零时的坐标.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由题,粒子恰能沿一定轨道做往复运动,分析可知,当t=2τ时刻,P在磁场中作圆周运动结束后并开始沿x轴负方向运动,才能沿一定的轨道作往复运动,画出轨迹,确定出粒子在磁场中圆周运动的周期,粒子在磁场中由洛伦兹力提供向心力,由牛顿第二定律和圆周运动的运动学公式求解B0应满足的关系;
(3)在t0(0<t0<τ/2)时刻释放P,P在电场中加速时间为τ-t0,由上题结果得到粒子在磁场中圆周运动的速度和半径,粒子又经过(τ-t0)时间速度减至零后向右加速时间为t0,根据几何知识求解P速度为零时的坐标.
解答:解:(1)由图2分析可知,在t=
τ时刻释放带电粒子P,在
τ~τ时间内做匀加速直线运动,τ~2τ时间内做匀速圆周运动,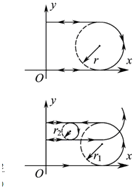
在电场中:粒子所受的电场力F=qE0,
根据牛顿第二定律得:加速度为a=
P在磁场中运动时速度的大小v0=at,t=
τ
解得,v0=
(2)只有当t=2τ时刻,P在磁场中作圆周运动结束后并开始沿x轴负方向运动,才能沿一定的轨道作往复运动,如图所示.设粒子在磁场中圆周运动的周期为T,则(n-
)T=τ,(n=1,2,3…)
粒子做匀速圆周运动时,有qvB0=m
,而T=
解得,B0=
,(n=1,2,3…)
(3)在t0时刻释放P,P在电场中加速时间为τ-t0,
在磁场中作匀速圆周运动的速度为 v1=
,
圆周运动的半径为 r1=
解得,r1=
又经(τ-t0)时间P减速为零后向右加速时间为t0,
P再次进入磁场速度为 v2=
圆周运动的半径为 r2=
解得,r2=
综上分析,速度为零时横坐标为 x=0
相应的纵坐标为 y=
,(k=1,2,3,…)
解得,y=
,(k=1,2,3,…)
答:
(1)P在磁场中运动时速度的大小v0为
.
(2)B0应满足的关系为B0=
,(n=1,2,3…);
(3)在t0(0<t0<τ/2)时刻释放P,P速度为零时横坐标为x=0,相应的纵坐标为y=
,(k=1,2,3,…).
| 1 |
| 2 |
| 1 |
| 2 |

在电场中:粒子所受的电场力F=qE0,
根据牛顿第二定律得:加速度为a=
| F |
| m |
P在磁场中运动时速度的大小v0=at,t=
| 1 |
| 2 |
解得,v0=
| qE0τ |
| 2m |
(2)只有当t=2τ时刻,P在磁场中作圆周运动结束后并开始沿x轴负方向运动,才能沿一定的轨道作往复运动,如图所示.设粒子在磁场中圆周运动的周期为T,则(n-
| 1 |
| 2 |
粒子做匀速圆周运动时,有qvB0=m
| v2 |
| r |
| 2πr |
| v |
解得,B0=
| (2n-1)πm |
| qτ |
(3)在t0时刻释放P,P在电场中加速时间为τ-t0,
在磁场中作匀速圆周运动的速度为 v1=
| qE0(τ-t0) |
| m |
圆周运动的半径为 r1=
| mv1 |
| qB0 |
解得,r1=
| E0(τ-t0) |
| B0 |
又经(τ-t0)时间P减速为零后向右加速时间为t0,
P再次进入磁场速度为 v2=
| qE0t0 |
| m |
圆周运动的半径为 r2=
| mv2 |
| qB0 |
解得,r2=
| E0t0 |
| B0 |
综上分析,速度为零时横坐标为 x=0
相应的纵坐标为 y=
|
解得,y=
|
答:
(1)P在磁场中运动时速度的大小v0为
| qE0τ |
| 2m |
(2)B0应满足的关系为B0=
| (2n-1)πm |
| qτ |
(3)在t0(0<t0<τ/2)时刻释放P,P速度为零时横坐标为x=0,相应的纵坐标为y=
|
点评:本题是带电粒子在复合场中运动的问题,分析粒子的受力情况,确定其运动情况,关键是运用几何知识求解坐标.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
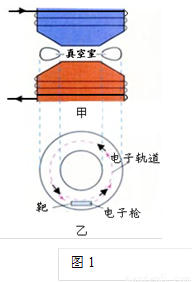
 现代科学研究中常要用到高速电子,电子感应加速器就是利用感生电场使电子加速的设备.它的基本原理如图甲所示,上、下为两个电磁铁,磁极之间有一个环形真空室,电子在真空中做圆周运动.电磁铁线圈电流的大小、方向可以变化,产生的感生电场使电子加速.图乙为真空室的俯视图.则下列说法正确的是( )
现代科学研究中常要用到高速电子,电子感应加速器就是利用感生电场使电子加速的设备.它的基本原理如图甲所示,上、下为两个电磁铁,磁极之间有一个环形真空室,电子在真空中做圆周运动.电磁铁线圈电流的大小、方向可以变化,产生的感生电场使电子加速.图乙为真空室的俯视图.则下列说法正确的是( )| A、如要使电子在真空室内沿如乙图所示逆时针方向加速,则电磁铁中应通以方向如图甲所示,大小增强的电流 | B、若要使电子在真空室内沿如乙图所示逆时针方向加速,则电磁铁中应通以方向如图甲所示方向相反,大小增强的电流 | C、在电子感应加速器中,电子只能沿逆时针方向加速 | D、该加速装置同样可以用来加速质子、α粒子等质量较大的带电粒子 |
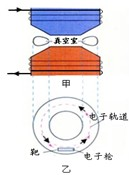 现代科学研究中常要用到高速电子,电子感应加速器就是利用感生电场使电子加速的设备.它的基本原理如图甲所示,上、下为两个电磁铁,磁极之间有一个环形真空室,电子在真空中做圆周运动.电磁铁线圈电流的大小、方向可以变化,产生的感生电场使电子加速.图乙为真空室的俯视图.则下列说法正确的是( )
现代科学研究中常要用到高速电子,电子感应加速器就是利用感生电场使电子加速的设备.它的基本原理如图甲所示,上、下为两个电磁铁,磁极之间有一个环形真空室,电子在真空中做圆周运动.电磁铁线圈电流的大小、方向可以变化,产生的感生电场使电子加速.图乙为真空室的俯视图.则下列说法正确的是( )| A、如要使电子在真空室内沿如乙图所示逆时针方向加速,则电磁铁中应通以方向如图甲所示,大小增强的电流 | B、若要使电子在真空室内沿如乙图所示逆时针方向加速,则电磁铁中应通以方向如图甲所示方向相反,大小增强的电流 | C、在电子感应加速器中,电子只能沿逆时针方向加速 | D、该加速装置不可以用来加速质子、α粒子等质量较大的带电粒子 |