题目内容
如图1所示, A、B、C、D为固定于竖直平面内的闭合绝缘轨道,AB段、CD段均为半径R=1.6m的半圆,BC、AD段水平,AD=BC=8m。B、C之间的区域存在水平向右的有界匀强电场,
场强E=5×105V/m。质量为m=4×10-3kg、带电量q=+1×10-8C的小环套在轨道上。小环与轨道AD段
的动摩擦因数为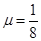 ,与轨道其余部分的摩擦忽略不计。现使小环在D点获得沿轨道向左的初速度
,与轨道其余部分的摩擦忽略不计。现使小环在D点获得沿轨道向左的初速度
v0=4m/s,且在沿轨道AD段运动过程中始终受到方向竖直向上、大小随速度变化的力F(变化关系如
图2)作用,小环第一次到A点时对半圆轨道刚好无压力。不计小环大小,g取10m/s2。求: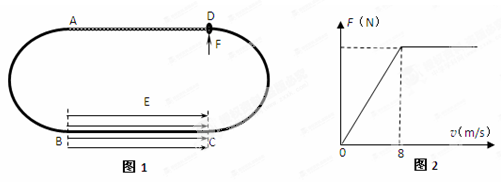
(1)小环运动第一次到A时的速度多大?
(2)小环第一次回到D点时速度多大?
(3)小环经过若干次循环运动达到稳定运动状态,此时到达D点时速度应不小于多少?
(1)4m/s;(2)6m/s;(3)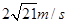
解析试题分析:(1)进入半圆轨道AB时小坏仅受重力,在A点由向心力公式得: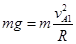
得:
(2) 小物块从D出发,第一次回到D的过程,由动能定理得: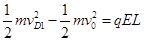
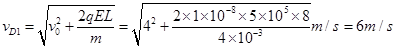
(3) 分析:初始位置D点时,若所加力F﹥mg ,则小坏受摩擦力而减速,同时F减小,当
F= mg时匀速,但速度一定小于4m/s;若F﹤mg, 则小坏受摩擦力而减速,同时F越来越小,摩擦力越来越大,小环继续减速直至静止,不会到达A点时速度为4m/s,综上可知小环第一次从D到A做匀速运动。
由图象知:F=kv=mg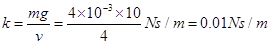
所以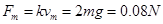 ,
,
则可知环与杆的摩擦力f≤μ|Fm-mg|=μmg=qE,
稳定循环时,每一个周期中损耗的能量应等于补充的能量
而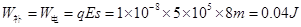
所以稳定循环运动时小环在AD段运动时速度一定要大于等于8m/s
即到达A点的速度不小于8m/s
稳定循环运动时小环从A到D的过程,由动能定理得: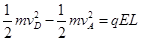
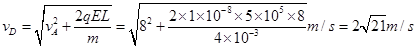
达到稳定运动状态时,小环到达D点时速度应不小于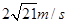
考点:动能定理;向心力公式


 L的杆水平放置,杆两端A、B系着长为3L的不可伸长且光滑的柔软轻绳,绳上套着一质量为m的小铁环.已知重力加速度为g.不计空气影响.
L的杆水平放置,杆两端A、B系着长为3L的不可伸长且光滑的柔软轻绳,绳上套着一质量为m的小铁环.已知重力加速度为g.不计空气影响.


 从O点沿粗糙的水平面向右运动,同时受到一水平向左的恒力F作用,物块在运动过程中速度随时间变化的规律如图乙所示,求:
从O点沿粗糙的水平面向右运动,同时受到一水平向左的恒力F作用,物块在运动过程中速度随时间变化的规律如图乙所示,求: