题目内容
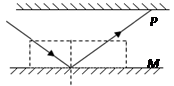
如图所示,一个半径为r的圆木板静止在水面上,在圆木板圆心O的正下方H=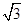 r处有一点光源S,已知水的折射率n=
r处有一点光源S,已知水的折射率n=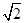 .
.
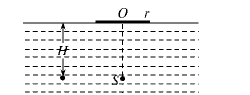
(1)求沿圆木板边缘出射的折射光线的折射角.
(2)若要在水面上方观察不到点光源S所发出的光,则应将点光源S至少竖直向上移多大的距离?(结果可用根式表示)
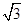 r处有一点光源S,已知水的折射率n=
r处有一点光源S,已知水的折射率n=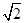 .
.
(1)求沿圆木板边缘出射的折射光线的折射角.
(2)若要在水面上方观察不到点光源S所发出的光,则应将点光源S至少竖直向上移多大的距离?(结果可用根式表示)
(1)45° (2)(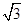 -1)r
-1)r
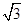 -1)r
-1)r(1)设入射角为θ1,折射角为θ2,则tanθ1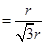 ①
①
即θ1=30°②
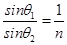 ③
③
联立①②③式得θ2=45°.④
(2)若在水面上方观察不到点光源所发出的光,则入射到圆木板边缘的光线将发生全反射,设临界角为C,点光源S离圆心的距离为h,则由sinC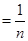 得⑤
得⑤
C=45°⑥
由几何关系tanC=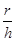 得⑦
得⑦
h=r⑧
则点光源S至少上移Δh=(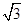 -1)r.⑨
-1)r.⑨
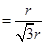 ①
①即θ1=30°②
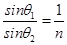 ③
③联立①②③式得θ2=45°.④
(2)若在水面上方观察不到点光源所发出的光,则入射到圆木板边缘的光线将发生全反射,设临界角为C,点光源S离圆心的距离为h,则由sinC
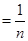 得⑤
得⑤C=45°⑥
由几何关系tanC=
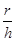 得⑦
得⑦h=r⑧
则点光源S至少上移Δh=(
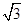 -1)r.⑨
-1)r.⑨
练习册系列答案
相关题目
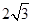 cm,已知玻璃砖的折射率n=
cm,已知玻璃砖的折射率n=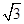 ,光在真空中的传播速度c=3×108m/s。求:①玻璃砖的厚度;②光在玻璃砖中运动时间。
,光在真空中的传播速度c=3×108m/s。求:①玻璃砖的厚度;②光在玻璃砖中运动时间。