��Ŀ����
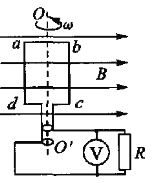
����Ŀ����ͼ��ʾ��ˮƽ���õ�U�ε����㹻�������ڷ�����ֱ���ϵ���ǿ�ų��У��Ÿ�Ӧǿ�ȴ�СΪB=5T���������L=0.4m�������R=0.5���Ķ�ֵ�������ӡ��Ҳ��е����ab����ڵ����ϣ������ab����m=2.0kg������r=0.5�����뵼��Ķ�Ħ��������=0.2���������ɺ��Բ��ơ������ab�ڴ�СΪ10N��ˮƽ����F�����£��ɾ�ֹ��ʼ�˶���x=40cm���ٶȴﵽ���ȡg=10m/s2.��
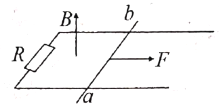
(1)�����ab�˶�������ٶ��Ƕ���?
(2)�������ab���ٶ�v=1msʱ�������ab�ļ��ٶ��Ƕ���?
(3)�����ab�ɾ�ֹ�ﵽ����ٶȵĹ����У�����R�ϲ����������Ƕ���?
���𰸡�(1)vm=1.5m/s (2)a=1m/s2 (3)QR=0.075J
��������
��1�������ab��ֱ�и�Ÿ��ߣ������ĵ綯�ƴ�С��E��BLv��
�ɱպϵ�·��ŷķ���ɵã�![]()
������ܵ��İ�������FA=BIL��
�������������ֱ���˶�ʱ�ٶ������ƽ�������ã�![]()
�������ٶȣ�vm=1.5m/s��
��2�����ٶ�Ϊv��ţ�ٵڶ����ɵã�![]()
��ã�a=1m/s2��
��3�������������У��������غ㶨�ɿɵ�:![]()
��ã�Q=0.15J��
����QR=0.075J��

��ϰ��ϵ�д�
 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
�����Ŀ