题目内容
19.对于平抛运动| 平抛运动的速度 | 平抛运动的位移 | |
| 示意图 | ||
| vx=v0 vy=gt v=$\sqrt{{v}_{0}^{2}+{g}^{2}{t}^{2}}$ tanθ=$\frac{gt}{{v}_{0}}$ | x=v0t y=$\frac{1}{2}g{t}^{2}$ s=$\sqrt{{v}_{0}^{2}{t}^{2}+\frac{1}{4}{g}^{2}{t}^{2}}$ tanα=$\frac{gt}{2{v}_{0}}$ |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据分位移和分速度公式求解即可.
解答 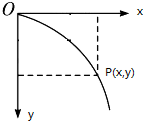 解:示意图如图.平抛运动在水平方向上做匀速直线运动,则有:vx=v0.x=v0t
解:示意图如图.平抛运动在水平方向上做匀速直线运动,则有:vx=v0.x=v0t
竖直方向上初速度为零,仅受重力,做自由落体运动,vy=gt.y=$\frac{1}{2}g{t}^{2}$.
合速度 v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=$\sqrt{{v}_{0}^{2}+{g}^{2}{t}^{2}}$,速度v与水平方向的夹角为θ,则tanθ=$\frac{{v}_{y}}{{v}_{x}}$=$\frac{gt}{{v}_{0}}$,s=$\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{{v}_{0}^{2}{t}^{2}+\frac{1}{4}{g}^{2}{t}^{2}}$,tanα=$\frac{y}{x}$=$\frac{gt}{2{v}_{0}}$
故答案为:v0,gt,$\sqrt{{v}_{0}^{2}+{g}^{2}{t}^{2}}$,$\frac{gt}{{v}_{0}}$,v0t,$\frac{1}{2}g{t}^{2}$.v0t;$\frac{1}{2}g{t}^{2}$,$\sqrt{{v}_{0}^{2}{t}^{2}+\frac{1}{4}{g}^{2}{t}^{2}}$,$\frac{gt}{2{v}_{0}}$.
点评 解决本题的关键知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,掌握分运动的规律.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
9.日常生活中谈到的“热”,具有不同的含义,它可以表示物理学中的热量、温度、内能等,以下叙述中哪个“热”是用来表示物理学上的内能( )
| A. | 今天的天气很热 | B. | 摩擦生热 | ||
| C. | 物体放热温度降低 | D. | 今年出现足球热 |
10.负点电荷周围的电场线如图所示,电场中有A、B两点,可以确定( )


| A. | A、B两点的电场强度大小相等 | |
| B. | B点的电势低于A点的电势 | |
| C. | B点的电场强度小于A点的电场强度 | |
| D. | 将同一点电荷分别放置于A、B两点,所受电场力大小相等 |
14.甲、乙两车在同一地点同时做直线运动,其v-t图象如图所示,则( )


| A. | 甲的加速度大于乙的加速度 | |
| B. | 0~t1时间内,甲的速度大于乙的速度 | |
| C. | 0~t1时间内,甲的位移大于乙的位移 | |
| D. | t1时刻甲、乙相遇 |
8.关于圆周运动的下列说法中正确的是( )
| A. | 做匀速圆周运动的物体,在任何相等的时间内通过的位移都相等 | |
| B. | 做匀速圆周运动的物体,转速n越大,角速度ω越小 | |
| C. | 向心加速度是描述线速度大小变化快慢的物理量 | |
| D. | 做圆周运动的物体所受合力不一定指向圆心 |
 如图所示,在空间存在垂直纸面向外的匀强磁场和方向竖直向上的匀强电场,电场强度为E,磁感应强度为B.在某点由静止释放一个带电液滴a,它运动到最低点处恰与原来静止在该处的带电液滴b相碰(b原来静止时只受重力和电场力),碰后两液滴合为一体,并沿水平方向做匀速直线运动.已知a的质量为b的质量的2倍,a的电量为b的电量的4倍,a与b间的库仑力可忽略不计.试求:
如图所示,在空间存在垂直纸面向外的匀强磁场和方向竖直向上的匀强电场,电场强度为E,磁感应强度为B.在某点由静止释放一个带电液滴a,它运动到最低点处恰与原来静止在该处的带电液滴b相碰(b原来静止时只受重力和电场力),碰后两液滴合为一体,并沿水平方向做匀速直线运动.已知a的质量为b的质量的2倍,a的电量为b的电量的4倍,a与b间的库仑力可忽略不计.试求: