题目内容
 如图在竖直平面内有水平向右、电场强度为E=1×104N/C的匀强电场.在匀强电场中有一根长L=2m的绝缘细线,一端固定在O点,另一端系一质量为m=0.04kg的带电小球,它静止A点时悬线与竖直方向成θ=37°角.若小球恰好绕点在竖直平面内做圆周运动,(cos37°=0.8g=10m/s2)试求:
如图在竖直平面内有水平向右、电场强度为E=1×104N/C的匀强电场.在匀强电场中有一根长L=2m的绝缘细线,一端固定在O点,另一端系一质量为m=0.04kg的带电小球,它静止A点时悬线与竖直方向成θ=37°角.若小球恰好绕点在竖直平面内做圆周运动,(cos37°=0.8g=10m/s2)试求:(1)小球的带电荷量Q
(2)小球动能的最小值
(3)小球机械能的最小值(取小球静止时的位置为电势能零点和重力势能零点)
分析:(1)根据小球在平衡位置合力为0,可以求出小球所受的电场力从而得出小球的带电荷量;
(2)根据小球恰好在竖直面内做圆周运动这一临界条件,知,在平衡位置处合外力提供圆周运动的向心力从而求出小球动能的最小值.
(3)抓住小球能量守恒,电势能最大处小球的机械能最小,根据做功情况分析.
(2)根据小球恰好在竖直面内做圆周运动这一临界条件,知,在平衡位置处合外力提供圆周运动的向心力从而求出小球动能的最小值.
(3)抓住小球能量守恒,电势能最大处小球的机械能最小,根据做功情况分析.
解答:解:(1)对小球进行受力分析如上图所示,
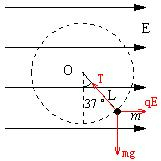
可得:
=tan37°.解得:小球的带电量为 q=
=3×10-5C.
(2)由于重力和电场力都是恒力,所以它们的合力也是恒力.
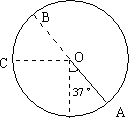
在圆上各点中,小球在平衡位置A点时的势能(重力势能和电势能之和)最小,在平衡位置的对称点B点,小球的势能最大,由于小球总能量不变,所以在B点的动能EkB最小,对应速度vB最小,在B点,小球受到的重力和电场力,其合力作为小球做圆周运动的向心力,而绳的拉力恰为零,有:
T=
=0.5N,而F合=
,所以EKB=
m
=
F合L=0.5J
(3)由于总能量保持不变,即Ek+EPG+EPE=恒量.所以当小球在圆上最左侧的C点时,电势能EPE最大,机械能最小.
由B运动到A,W合力=-(EPA-EPB),W合力=F合?2L,所以EPB=2J
总能量E=EPB+EkB=2.5J.
由C→A,WFE=FE?L?(1+sin37°)=0.96J,WFE=EP2 (EP2为C点电势能)
所以C点的机械能为E机C=E-EP2=1.54J
答:(1)小球的带电荷量Q=3×10-5C
(2)小球动能的最小值Ekmin=0.5J
(3)小球机械能的最小值(取小球静止时的位置为电势能零点和重力势能零点)Emin=1.54J

可得:
| qE |
| mg |
| mgtan37° |
| E |
(2)由于重力和电场力都是恒力,所以它们的合力也是恒力.

在圆上各点中,小球在平衡位置A点时的势能(重力势能和电势能之和)最小,在平衡位置的对称点B点,小球的势能最大,由于小球总能量不变,所以在B点的动能EkB最小,对应速度vB最小,在B点,小球受到的重力和电场力,其合力作为小球做圆周运动的向心力,而绳的拉力恰为零,有:
T=
| mg |
| cos37° |
m
| ||
| L |
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
(3)由于总能量保持不变,即Ek+EPG+EPE=恒量.所以当小球在圆上最左侧的C点时,电势能EPE最大,机械能最小.
由B运动到A,W合力=-(EPA-EPB),W合力=F合?2L,所以EPB=2J
总能量E=EPB+EkB=2.5J.
由C→A,WFE=FE?L?(1+sin37°)=0.96J,WFE=EP2 (EP2为C点电势能)
所以C点的机械能为E机C=E-EP2=1.54J
答:(1)小球的带电荷量Q=3×10-5C
(2)小球动能的最小值Ekmin=0.5J
(3)小球机械能的最小值(取小球静止时的位置为电势能零点和重力势能零点)Emin=1.54J
点评:该题为小球在电场和重力场这一复合场中的运动问题,抓住重力和电场力的合力为恒力这一突破口解决本题.

练习册系列答案
相关题目
 如图,质量为0.5kg的小杯里盛有1kg的水,用绳子系住小杯在竖直平面内做“水流星”表演,转动半径为1m,小杯通过最高点的速度为4m/s,g取10m/s2.求:
如图,质量为0.5kg的小杯里盛有1kg的水,用绳子系住小杯在竖直平面内做“水流星”表演,转动半径为1m,小杯通过最高点的速度为4m/s,g取10m/s2.求: 如图,质量为0.5kg的小杯里盛有1kg的水,用绳子系住小杯在竖直平面内做“水流星”表演,转动半径为1m,g取10m/s.求:
如图,质量为0.5kg的小杯里盛有1kg的水,用绳子系住小杯在竖直平面内做“水流星”表演,转动半径为1m,g取10m/s.求: 如图,质量为0.5kg的杯子里盛有1kg的水,用绳子系住水杯在竖直平面内做“水流星”表演,转动半径为1m,水杯通过最高点的速度为4m/s,求:
如图,质量为0.5kg的杯子里盛有1kg的水,用绳子系住水杯在竖直平面内做“水流星”表演,转动半径为1m,水杯通过最高点的速度为4m/s,求: 如图所示,杯子里盛有m2=1kg的水,用绳子系住水杯在竖直平面内做“水流星”表演,转动半径为r=1m,水杯通过最高点的速度为v=4m/s,求:在最高点时,水对杯底的压力.
如图所示,杯子里盛有m2=1kg的水,用绳子系住水杯在竖直平面内做“水流星”表演,转动半径为r=1m,水杯通过最高点的速度为v=4m/s,求:在最高点时,水对杯底的压力.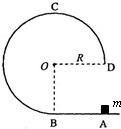 如图所示,在竖直平面内有一固定轨道,其中AB是长为R的粗糙水平直轨道,BCD是圆心为O、半径为R的3/4光滑圆弧轨道,两轨道相切于B点.在推力作用下,质量为m的小滑块从A点由静止开始做匀加速直线运动,到达B点时即撤去推力,小滑块恰好能沿圆轨道经过最高点C.重力加速度大小为g.则小滑块( )
如图所示,在竖直平面内有一固定轨道,其中AB是长为R的粗糙水平直轨道,BCD是圆心为O、半径为R的3/4光滑圆弧轨道,两轨道相切于B点.在推力作用下,质量为m的小滑块从A点由静止开始做匀加速直线运动,到达B点时即撤去推力,小滑块恰好能沿圆轨道经过最高点C.重力加速度大小为g.则小滑块( )