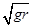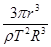题目内容
嫦娥四号，专家称“四号星”，计划在2017年发射升空，它是嫦娥探月工程计划中嫦娥系列的第四颗人造探月卫星，主要任务是更深层次、更加全面的科学探测月球地貌、资源等方面的信息，完善月球档案资料．已知月球的半径为R，月球表面的重力加速度为g，月球的平均密度为ρ，嫦娥四号离月球中心的距离为r，绕月周期为T．根据以上信息下列说法正确的是（ ）
分析：1、根据重力提供向心力mg=m
，得月球的第一宇宙速度为v=
．
2、根据万有引力提供向心力G
=m
，得v=
，月球表面的物体受到的重力等于万有引力mg=
，得GM=R2g．二式化简可得卫星速度．
3、根据万有引力提供向心力G
=m
r，得月球的质量M=
，解得月球的密度ρ=
=
=
，变形可得万有引力常量．
4、嫦娥四号必须加速做离心运动才能脱离月球束缚返回地球．
| v2 |
| R |
| gR |
2、根据万有引力提供向心力G
| Mm |
| r2 |
| v2 |
| r |
|
| GMm |
| R2 |
3、根据万有引力提供向心力G
| Mm |
| r2 |
| 4π2 |
| T2 |
| 4π2r3 |
| GT2 |
| M |
| V |
| ||
|
| 3πr3 |
| GT2R3 |
4、嫦娥四号必须加速做离心运动才能脱离月球束缚返回地球．
解答：解：A、月球的第一宇宙速度为近月卫星的运行速度，所以重力提供向心力mg=m
，得v=
．故A错误．
B、根据万有引力提供向心力G
=m
，得v=
，又因为月球表面的物体受到的重力等于万有引力mg=
，得GM=R2g．
所以v=
=
，故B错误．
C、根据万有引力提供向心力G
=m
r，得月球的质量M=
，所以月球的密度ρ=
=
=
，所以万有引力常量为G=
．故C正确．
D、嫦娥四号要脱离月球的束缚才能返回月球，嫦娥四号要脱离月球束缚必须加速做离心运动才行．故D错误．
故选：C．
| v2 |
| R |
| gR |
B、根据万有引力提供向心力G
| Mm |
| r2 |
| v2 |
| r |
|
| GMm |
| R2 |
所以v=
|
|
C、根据万有引力提供向心力G
| Mm |
| r2 |
| 4π2 |
| T2 |
| 4π2r3 |
| GT2 |
| M |
| V |
| ||
|
| 3πr3 |
| GT2R3 |
| 3πr3 |
| ρT2R3 |
D、嫦娥四号要脱离月球的束缚才能返回月球，嫦娥四号要脱离月球束缚必须加速做离心运动才行．故D错误．
故选：C．
点评：解决本题的关键掌握万有引力提供向心力G
=m
=m
r，会根据该规律计算线速度和中心天体的质量．
| Mm |
| r2 |
| v2 |
| r |
| 4π2 |
| T2 |
练习册系列答案
阅读快车系列答案
相关题目
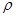，嫦娥四号离月球中心的距离为r，绕月周期为T。根据以上信息下列说法正确的是
