题目内容
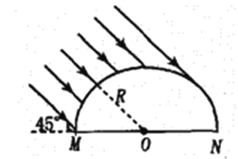
【题目】将长为l的玻璃圆柱体沿轴剖开后得到一块半圆柱体，其截面的正视图如图所示，MNPQ为其底面(PQ图中未画出)，MN为直径。已知半圆的圆心为O、半径为R，玻璃的折射率n=
，一束与MNPQ所在平面成45°且垂直于轴的平行光射到半圆柱面上，经折射后，有部分光能从MNPQ面射出，忽略经多次反射到达MNPQ面的光线。求MNPQ透光部分的面积。
【答案】
【解析】设光由介质射向空气的临界角为C．由 sinC=
，得 C=45°
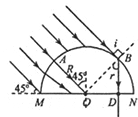
从A点进入玻璃砖的光线垂直半球面，沿半径AO直达球心O，且入射角等于临界角，恰好在O点发生全反射，A点左侧的光线经球面折射后，射在MN上的入射角都大于临界角，在MN上全反射，不能从MN上射出．A点右侧光线一直到与球面正好相切的范围内的光线经球面折射后，在MN上的入射角均小于临界角，都能从MN上射出，它们在MN上的出射宽度就是OD．由折射定律得
MN上透光部分的长度：OD=Rsinr
MNPQ平面内透光部分面积为：S=ODl=
Rl
练习册系列答案
黄冈创优卷系列答案
相关题目
