题目内容
12.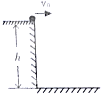 如图,平台高h=5m,小球以v0=10m/s的速度水平抛出,忽略空气阻力,求小球:
如图,平台高h=5m,小球以v0=10m/s的速度水平抛出,忽略空气阻力,求小球:(1)落地时间t;
(2)落地时水平位移x;
(3)落地时速度大小v;(g=10m/s2)
分析 根据高度求出平抛运动的时间,结合初速度和时间求出水平位移,根据竖直分速度、水平分速度,结合平行四边形定则求出落地的速度大小.
解答 解:(1)根据h=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×5}{10}}s=1s$.
(2)落地时水平位移x=v0t=10×1m=10m.
(3)竖直分速度vy=gt=10×1m/s=10m/s,
根据平行四边形定则知,落地的速度v=$\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=\sqrt{100+100}m/s=10\sqrt{2}m/s$.
答:(1)落地的时间为1s.
(2)落地时水平位移为10m.
(3)落地的速度大小为$10\sqrt{2}m/s$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
2.甲、乙两根金属丝,电阻率和长度均相同,甲的横截面积是乙的3倍,将它们并联在电池两端,下列判断正确的是( )
| A. | 甲、乙的电阻之比是1:3 | B. | 甲、乙的电阻之比是3:1 | ||
| C. | 甲、乙消耗的电功率之比是1:3 | D. | 甲、乙消耗的电功率之比是3:1 |
20. 如图所示,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的小滑 轮O,斜面体的倾角为30°,置于水平地面上.A的质量为m,B的质量为4m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中,斜面体始终保持静止,下列判断中正确的是( )
如图所示,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的小滑 轮O,斜面体的倾角为30°,置于水平地面上.A的质量为m,B的质量为4m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中,斜面体始终保持静止,下列判断中正确的是( )
 如图所示,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的小滑 轮O,斜面体的倾角为30°,置于水平地面上.A的质量为m,B的质量为4m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中,斜面体始终保持静止,下列判断中正确的是( )
如图所示,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的小滑 轮O,斜面体的倾角为30°,置于水平地面上.A的质量为m,B的质量为4m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中,斜面体始终保持静止,下列判断中正确的是( )| A. | 物块B受到的摩擦力先减小后增大 | |
| B. | 地面对斜体的摩擦力方向一直向左 | |
| C. | 小球A的机械能不守恒,A、B系统的机械能守恒 | |
| D. | 小球A的机械能守恒 |
7. 如图所示,测力计、绳子、滑轮的质量和摩擦均忽略不计.A、B均静止,已知GA=40N,GB=30N,以下判断正确的是( )
如图所示,测力计、绳子、滑轮的质量和摩擦均忽略不计.A、B均静止,已知GA=40N,GB=30N,以下判断正确的是( )
 如图所示,测力计、绳子、滑轮的质量和摩擦均忽略不计.A、B均静止,已知GA=40N,GB=30N,以下判断正确的是( )
如图所示,测力计、绳子、滑轮的质量和摩擦均忽略不计.A、B均静止,已知GA=40N,GB=30N,以下判断正确的是( )| A. | 测力计的示数为60N | B. | 测力计的示数为30N | ||
| C. | 地面对A的支持力为40N | D. | 物体A所受合力为30N |
17. 如图所示,光滑但质量分布不均匀球体的球心在O点,重心在P点.静止在竖直墙和桌边之间.桌边A点对球的弹力为F1,竖直墙对球的弹力为F2,现将球绕O点沿逆时针旋转180°,此时桌边A点对球的弹力为F1′,竖直墙对球的弹力为F2′,则下面结论正确的有( )
如图所示,光滑但质量分布不均匀球体的球心在O点,重心在P点.静止在竖直墙和桌边之间.桌边A点对球的弹力为F1,竖直墙对球的弹力为F2,现将球绕O点沿逆时针旋转180°,此时桌边A点对球的弹力为F1′,竖直墙对球的弹力为F2′,则下面结论正确的有( )
 如图所示,光滑但质量分布不均匀球体的球心在O点,重心在P点.静止在竖直墙和桌边之间.桌边A点对球的弹力为F1,竖直墙对球的弹力为F2,现将球绕O点沿逆时针旋转180°,此时桌边A点对球的弹力为F1′,竖直墙对球的弹力为F2′,则下面结论正确的有( )
如图所示,光滑但质量分布不均匀球体的球心在O点,重心在P点.静止在竖直墙和桌边之间.桌边A点对球的弹力为F1,竖直墙对球的弹力为F2,现将球绕O点沿逆时针旋转180°,此时桌边A点对球的弹力为F1′,竖直墙对球的弹力为F2′,则下面结论正确的有( )| A. | F1>F1′,F2>F2′ | B. | F1=F1′,F2=F2′ | C. | F1<F1′,F2<F2′ | D. | F1<F1′,F2=F2′ |
 如图所示,在y轴右方有方向垂直于纸面的匀强磁场,一个质量为m,电量为q的质子以速度v水平向右经过x轴上的P点最后从y轴上的M点射出,已知M点到原点的距离为L,质子射出磁场时的速度方向与y轴的夹角θ为30°.求:
如图所示,在y轴右方有方向垂直于纸面的匀强磁场,一个质量为m,电量为q的质子以速度v水平向右经过x轴上的P点最后从y轴上的M点射出,已知M点到原点的距离为L,质子射出磁场时的速度方向与y轴的夹角θ为30°.求: 一质量为1kg的物体在恒力F作用下从水平地面上的A点由静止开始向C点运动,其中AB段光滑,BC段粗糙,物体运动到B点后立即做匀速运动,已知AC间距为100m,物体由A点运动到C点共用11s,物体在AB段运动的第2s内通过的距离为7.5m.
一质量为1kg的物体在恒力F作用下从水平地面上的A点由静止开始向C点运动,其中AB段光滑,BC段粗糙,物体运动到B点后立即做匀速运动,已知AC间距为100m,物体由A点运动到C点共用11s,物体在AB段运动的第2s内通过的距离为7.5m.