题目内容
14. 如图所示,皮带传动装置与水平面夹角为37°,两轮轴心相距L=5.8m,A、B分别使传送带与两轮的切点,轮缘与传送带之间不打滑,质量为0.1kg的小物块与传送带间的动摩擦因数为μ=0.5.传送带沿逆时针方向以v1=2m/s的速度匀速运动时,将小物块无初速地放在A点后,它会运动至B点.(g取10m/s2))
如图所示,皮带传动装置与水平面夹角为37°,两轮轴心相距L=5.8m,A、B分别使传送带与两轮的切点,轮缘与传送带之间不打滑,质量为0.1kg的小物块与传送带间的动摩擦因数为μ=0.5.传送带沿逆时针方向以v1=2m/s的速度匀速运动时,将小物块无初速地放在A点后,它会运动至B点.(g取10m/s2))(1)求物体刚放在A点的加速度?
(2)物体从A到B约需多长时间?
(3)小物块相对于传送带运动时,会在传送带上留下痕迹.求小物块在传送带上留下的痕迹长度?
分析 (1)由牛顿第二定律可以求出加速度;
(2)小物块向下加速运动当速度达到传送带速度时判定小物块是否到达底端,如若没有则小物块摩擦力会改变方向,再根据牛顿第二定律求解小物块的运动情况,从而分段求出小物块的运动时间即可;
(3)小物块在传送带上留下痕迹的长度即为小物块相对于传送带的位移大小.
解答 解:(1)物体刚放在A点时相对于传送带向上滑动,受到沿传送带向下的滑动摩擦力,
由牛顿第二定律得:mgsin37°+μmgcos37°=ma1 ,解得 a1=10m/s2;
(2)物块开始沿传送带向下做匀加速直线运动,当速度与传送带速度相等时,
需要的时间:t1=$\frac{{v}_{1}}{{a}_{1}}$=0.2s,位移:x1=$\frac{{v}_{1}}{2}$t1=0.2m<L=5.8m,
然后物块相对于传送带向下运动,受到向上的摩擦力作用,
由牛顿第二定律得:mgsin37°-μmgcos37°=ma2 ,解得:a2=2m/s2,
物体到达底端过程中,由匀变速直线运动的位移公式得:
x2=L-x1=v1t2+$\frac{1}{2}$a2t22 ,解得:t2=1.57s,
物块由静止出发从A到B所用时间为:t=t1+t2=1.77s;
(3)物块运动过程传送带的位移:x=v1t=3.14m,
小物块在传送带上留下的痕迹长度:△x=L-x=2.66m;
答:(1)物体刚放在A点的加速度为10m/s2;
(2)物体从A到B约需要1.77s;
(3)小物块在传送带上留下的痕迹长度为2.66m.
点评 本题考查了牛顿第二定律的应用,分析清楚物块的运动过程是解题的关键,应用牛顿第二定律与运动学公式可以解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.关于重力和弹力,下列说法正确的是( )
| A. | 重力总是垂直向下 | |
| B. | 两个物体只要相互接触就会产生弹力 | |
| C. | 形状规则的物体的重心一定与其几何中心重合 | |
| D. | 物体对桌面的压力是由于物体发生弹性形变而产生的 |
9.下列物体中处于平衡状态的是( )
| A. | 从空中自由下落的纸片 | |
| B. | 糙斜面上匀速下滑的物体 | |
| C. | 在狂风中摇晃的树 | |
| D. | 正在减速行驶的汽车 | |
| E. | 静止在粗糙斜面上的物体 | |
| F. | 做自由落体运动的物体在刚开始下落的一瞬间 |
19.如图,在粗糙的水平面上放置一个小物体P,P受到与水平面成夹角θ的斜向上的拉力F用沿水平面运动,如图甲所示,物体P的加速度随F变化规律如图乙中图线P所示.把物体P换成物体Q,其他不变,重复操作,得到Q的加速度随F变化规律如图乙中图线Q所示.图乙中b、c和d为已知量,由此可知( ) 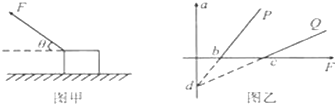

| A. | P的质量小于Q的质量 | B. | P和Q的材料不同 | ||
| C. | 根据图象能求出角θ(三角函数值) | D. | Q的质量为-$\frac{d}{c}$ |
3.小物块随足够长的水平传送带一起运动,被一水平向左飞来的子弹击中并从物块中穿过(子弹与物块作用时间极短),如图1所示.固定在传送带右端的位移传感器纪录了小物块被击中后的位移x随时间t的变化关系图象如图2所示(图象前3s内为二次函数,3-4.5s内为一次函数,取向左运动的方向为正方向).已知传送带的速度保持不变,g取10m/s2.下列说法正确的是( )
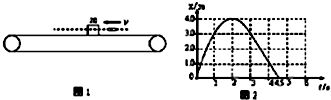

| A. | 物块被子弹击中后向左运动的初速度是4m/s | |
| B. | 传送带与物块间的动摩擦因数为0.1 | |
| C. | 传送带的速度大小为1m/s | |
| D. | 物块在传送带上滑过的痕迹是9m |
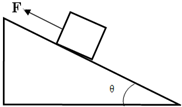 如图所示,将一质量为m=2kg的物块放在倾角为θ=37°的斜面上,在物块上加一平行于斜面向上拉力F使物体处在静止状态,已知物体与斜面间的动摩擦因数为μ=0.5,假设物体与斜面间的滑动摩擦力等于最大静摩擦力,求F大小范围.(已知sin37°=0.6,cos37°=0.8;g=10m/s2)
如图所示,将一质量为m=2kg的物块放在倾角为θ=37°的斜面上,在物块上加一平行于斜面向上拉力F使物体处在静止状态,已知物体与斜面间的动摩擦因数为μ=0.5,假设物体与斜面间的滑动摩擦力等于最大静摩擦力,求F大小范围.(已知sin37°=0.6,cos37°=0.8;g=10m/s2)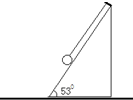 如图,倾角为53°的光滑斜面置于光滑水平面上,其顶端用细线一质量m=0.5kg的小球,已知sin53°=0.8,cos53°=0.6,g=10N/kg
如图,倾角为53°的光滑斜面置于光滑水平面上,其顶端用细线一质量m=0.5kg的小球,已知sin53°=0.8,cos53°=0.6,g=10N/kg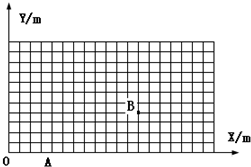 质量m=1kg的质点开始静止在xoy平面上原点O,某一时刻受到沿+x方向恒力F1=2N的作用.若力F1作用一段时间t1到达A点(图上位置未知)后撤去,立即施加沿y轴方向的力F2,再经时间t2=2s,质点恰好通过该平面上的B点,如图所示,B点的坐标为x=12m,y=4m.在B点时撤去F2并立即施加力F3,经过t3=2s质点到达C时速度刚好为零.不计其它作用.
质量m=1kg的质点开始静止在xoy平面上原点O,某一时刻受到沿+x方向恒力F1=2N的作用.若力F1作用一段时间t1到达A点(图上位置未知)后撤去,立即施加沿y轴方向的力F2,再经时间t2=2s,质点恰好通过该平面上的B点,如图所示,B点的坐标为x=12m,y=4m.在B点时撤去F2并立即施加力F3,经过t3=2s质点到达C时速度刚好为零.不计其它作用. 如图所示一倾角为θ=60°的光滑斜面,下端与一段很短的光滑弧面相切,弧面另一端与水平传送带相切,水平传送带以5m/s的顺时针转动,今有如图所示一光滑的斜面,下端与一段很短的光滑孤面相切,孤面另一端与水平传送带相切,水平传送带以5m/s顺时针转动,今有质量为1kg的物体(可视为质点)从斜面上高度为h=5m处滑下,物体在孤面运动时不损失机械能,而且每次在孤面上运动时间极短可以忽略,已知传送带足够长,它与物体之间的滑动摩擦因数为0.5.取g=10m/s2 求:
如图所示一倾角为θ=60°的光滑斜面,下端与一段很短的光滑弧面相切,弧面另一端与水平传送带相切,水平传送带以5m/s的顺时针转动,今有如图所示一光滑的斜面,下端与一段很短的光滑孤面相切,孤面另一端与水平传送带相切,水平传送带以5m/s顺时针转动,今有质量为1kg的物体(可视为质点)从斜面上高度为h=5m处滑下,物体在孤面运动时不损失机械能,而且每次在孤面上运动时间极短可以忽略,已知传送带足够长,它与物体之间的滑动摩擦因数为0.5.取g=10m/s2 求: