��Ŀ����
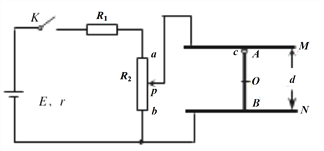
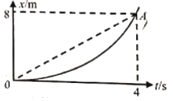
����Ŀ��ͬһˮƽ���ϵ���������ƽ�н���ֱ���MN��M��N������ͼ��ʾ���ã������֮��ľ���l=0.5m�������M M����֮���һ��ֵR=0.4���Ķ�ֵ���裬����ĵ���ɺ��Բ��ƣ�N N����������λ����ֱ���ڵİ�Բ�ι⻬�������NP��N��P��ƽ�����ӣ�����Բ����İ뾶��ΪR0=0.5m��ˮƽֱ���MR��M��R���δֲڣ�RN��R��N���ι⻬����RNN��R������ǡ�ô�����ֱ���µ���ǿ�ų��У��Ÿ�Ӧǿ��B=0.64T���ų�����Ŀ���d=1m�������ұ߽���NN���غϣ�����һ����m=0.2kg������r=0.1���ĵ����ab��ֹ�ھ�ų���߽�s=2m��������˴�ֱ��ˮƽ����F=2N�����¿�ʼ�˶��������ab��ֲڵ����Ķ�Ħ��������=0.1�����˶����ų�����߽�ʱ��ȥF����������abǡ����ͨ����Բ�ι������ߵ�PP������֪��������˶�����������ʼ�մ�ֱ�ҽӴ����ã�ȡg=10m/s2��
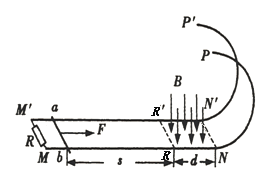
(1)����˸ս���ų�ʱ��ͨ��������ϵĵ�����С�ͷ���
(2)����˴����ų��Ĺ�����ͨ������R�ϵĵ����
(3)����˴����ų��Ĺ�����������·�в����Ľ����ȡ�
���𰸡���1��3.84A,��b��a��2��0.64C��3��1.1J
��������
(1) Ӧ�ö��ܶ����������ų�ʱ���ٶȣ����������ų�ʱ�������и�Ÿ��ߣ�������Ӧ�������ɷ����ڵ�Ÿ�Ӧ���ɺͱպϵ�·ŷķ���ɿ���ø�Ӧ������С�������ֶ����жϸ�Ӧ��������
(2) �赼����ڴų����˶���ʱ��Ϊt����������ĸ�Ӧ�綯�Ƶ�ƽ��ֵ������ŷķ�������������ƽ��ֵ���������������
(3)����˴����ų��Ĺ�������·�л�е��ת��Ϊ���ܣ����������غ㶨�������·�в����Ľ�������
(1)�赼�����F���������˶����ų�����߽�ʱ���ٶ�Ϊv1���ɶ��ܶ����ã�
![]()
�������ݽ��![]()
����˸ս���ų�ʱ�����ĸ�Ӧ�綯��![]()
��ʱͨ��������ϵĵ���![]()
�����ֶ����֪������������b��a
(2) �赼����ڴų����˶���ʱ��Ϊt�������ĸ�Ӧ�綯�Ƶ�ƽ��ֵΪ![]() ���ɷ����ڵ�Ÿ�Ӧ��������
���ɷ����ڵ�Ÿ�Ӧ��������
![]()
ͨ������R�ĸ�Ӧ������ƽ��ֵ![]()
ͨ������R�ĵ����![]()
(3) �赼����뿪�ų�ʱ���ٶȴ�СΪv2���˶���Բ�����ߵ���ٶ�Ϊv3�������ǡ����ͨ����Բ�ι������ߵ㣬���ڹ����ߵ�ʱ����ţ�ٵڶ����ɵã�
![]()
�������ݽ����![]()
�˴�NN���˶���PP���Ĺ��̣����ݻ�е���غ㶨������![]()
�������ݽ�ã�![]()
����˴����ų��Ĺ�������ʧ�Ļ�е��![]()
�˹����е�·�в����Ľ�����![]()