题目内容
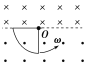
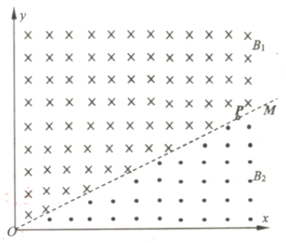
【题目】如图所示，在xOy平面的第I象限中，磁场分界线OM的上下两侧分别有垂直纸面向里、向外的匀强磁场B1和B2，磁感应强度大小B1=B2=B.质量为m，电量为-q的粒子速度一定，从O点沿x轴正方向垂直射入磁场，在磁场中运动的半径为d.已知粒子重力不计，磁场分布区域的大小可以通过调节分界线OM与x轴间的夹角改变.
(1)求粒子运动速度
的大小；
(2)欲使粒子从y轴射出，求分界线OM与x轴的最小夹角
；
(3)若分界线OM与x轴的夹角
=30°，将下方磁场的磁感应强度大小变为
，P是OM上一点，粒子恰能通过P点，求粒子从O点运动到P点时间
.
【答案】(1)
(2)75°(3)若粒子从上面磁场中经过P点，则粒子从O点运动到P点时间
(n=1、2、3….)；若粒子从下面磁场中经过P点，则粒子从O点运动到P点时间
(n=0、1、2、3….)
【解析】
(1)根据
且
r=d
解得
(2)欲使粒子恰好从y轴射出，则轨迹如图
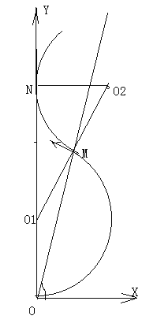
由几何关系可知
，则
，则分界线OM与x轴的最小夹角
(3)将下方磁场的磁感应强度大小变为
，则根据
则运动半径变为
，轨迹如图；
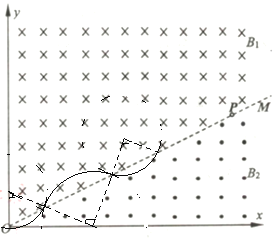
粒子在上下磁场中运动的周期分别为
在上下磁场中每次运动的时间分别为
若粒子从上面磁场中经过P点，则粒子从O点运动到P点时间
(n=1、2、3….)
若粒子从下面磁场中经过P点，则粒子从O点运动到P点时间
(n=0、1、2、3….)
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
