题目内容
(2008?绵阳模拟)假设质量为m 的人造地球卫星在圆轨道上运动,它离地面的高度是地球半径R 的2 倍,地球表面的重力加速度为g,则卫星的( )
分析:地球对人造卫星的万有引力提供其做圆周运动需要的向心力G
=mω2r=m
=ma,解出角速度、线速度、加速度的表达式.再根据地球表面的物体受到的重力等于万有引力mg=G
,得到GM=R2g,以及r=3R,化简可得到角速度、线速度、加速度的值.动能运用解得速度直接计算即可.
| Mm |
| r2 |
| v2 |
| r |
| Mm |
| R2 |
解答:解:A、根据万有引力提供向心力G
=mω2r
所以ω=
地球表面的物体受到的重力等于万有引力mg=G
,解得GM=R2g
所以ω=
,
因为r=3R
所以ω=
=
,故A正确.
B、根据万有引力提供向心力G
=m
所以v=
地球表面的物体受到的重力等于万有引力mg=G
,解得GM=R2g
所以v=
因为r=3R
所以v=
=
,故B错误.
C、根据万有引力提供向心力G
=ma
所以a=
地球表面的物体受到的重力等于万有引力mg=G
,解得GM=R2g
所以a=
因为r=3R
所以a=
=
,故C正确.
D、动能为Ek=
mv2=
m(
)2=
,故D错误.
故选:AC.
| Mm |
| r2 |
所以ω=
|
地球表面的物体受到的重力等于万有引力mg=G
| Mm |
| R2 |
所以ω=
|
因为r=3R
所以ω=
|
|
B、根据万有引力提供向心力G
| Mm |
| r2 |
| v2 |
| r |
所以v=
|
地球表面的物体受到的重力等于万有引力mg=G
| Mm |
| R2 |
所以v=
|
因为r=3R
所以v=
|
|
C、根据万有引力提供向心力G
| Mm |
| r2 |
所以a=
| GM |
| r2 |
地球表面的物体受到的重力等于万有引力mg=G
| Mm |
| R2 |
所以a=
| R2g |
| r2 |
因为r=3R
所以a=
| R2g |
| 9R2 |
| g |
| 9 |
D、动能为Ek=
| 1 |
| 2 |
| 1 |
| 2 |
|
| mgR |
| 6 |
故选:AC.
点评:本题要掌握两个关系:1、环绕天体做圆周运动所需要的向心力由万有引力提供,2、星球表面的物体受到的重力等于万有引力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
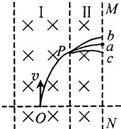 (2008?绵阳模拟)如图所示,匀强磁场的方向垂直纸面向里,一不计重力的带电微粒从o点竖直向上垂直于磁场方向射人,沿曲线opa垂直打到竖直屏MN上的a 点,通过Pa 段用时为t.若保持区域I 内匀强磁场不变,只增大区域Ⅱ内匀强磁场的磁感应强度大小,则微粒经过P点后运动的( )
(2008?绵阳模拟)如图所示,匀强磁场的方向垂直纸面向里,一不计重力的带电微粒从o点竖直向上垂直于磁场方向射人,沿曲线opa垂直打到竖直屏MN上的a 点,通过Pa 段用时为t.若保持区域I 内匀强磁场不变,只增大区域Ⅱ内匀强磁场的磁感应强度大小,则微粒经过P点后运动的( ) (2008?绵阳模拟)一质量为m、带正电的粒子从0 点竖直向上进人虚线框内的水平方向的匀强电场中,其运动轨迹如图所示,P点为轨迹的最高点,则( )
(2008?绵阳模拟)一质量为m、带正电的粒子从0 点竖直向上进人虚线框内的水平方向的匀强电场中,其运动轨迹如图所示,P点为轨迹的最高点,则( )