题目内容
20. 如图所示,在x轴下方的第Ⅲ、Ⅳ象限中,存在垂直于xOy平面方向的匀强磁场,磁感应强度B1=2B2=2B,带电粒子a、b分别从x轴上的P、Q两点(图中没有标出)以垂直于x轴方向的速度同时进入匀强磁场B1、B2中,两粒子恰在第一次通过y轴时发生正撞,碰撞前带电粒子a的速度方向与y轴正方向成60°角,若两带电粒子的比荷分别为k1、k2,进入磁场时的速度大小分别为v1、v2,不计粒子重力和两粒子间相互作用,则下列关系正确的是( )
如图所示,在x轴下方的第Ⅲ、Ⅳ象限中,存在垂直于xOy平面方向的匀强磁场,磁感应强度B1=2B2=2B,带电粒子a、b分别从x轴上的P、Q两点(图中没有标出)以垂直于x轴方向的速度同时进入匀强磁场B1、B2中,两粒子恰在第一次通过y轴时发生正撞,碰撞前带电粒子a的速度方向与y轴正方向成60°角,若两带电粒子的比荷分别为k1、k2,进入磁场时的速度大小分别为v1、v2,不计粒子重力和两粒子间相互作用,则下列关系正确的是( )| A. | k1=2k2 | B. | 2k1=k2 | C. | v1=2v2 | D. | 2v1=v2 |
分析 两个粒子均做匀速圆周运动,先画出轨迹,结合几何关系得到轨道半径关系;然后运用洛伦兹力等于向心力和时间关系列式求解比荷之比和速度之比.
解答 解:两个粒子均做匀速圆周运动,在通过y轴时发生正撞,轨迹如图所示:
显然两个粒子的电性相反,轨道半径相等;
洛伦兹力提供向心力,故:
$qvB=m\frac{{v}^{2}}{r}$
解得:
r=$\frac{mv}{qB}=\frac{v}{kB}$
故$\frac{{v}_{1}}{{k}_{1}{B}_{1}}=\frac{{v}_{2}}{{k}_{2}{B}_{2}}$ ①
运动时间相等,故:
$\frac{\frac{π}{3}•r}{{v}_{1}}$=$\frac{\frac{2}{3}π•r}{{v}_{2}}$ ②
根据题意,有:
B1=2B2=2B ③
联立解得:
2v1=v2
4k1=k2
故ABC错误,D正确;
故选:D
点评 本题关键是画出轨迹,结合几何关系得到半径关系,然后根据洛伦兹力等于向心力列式分析,不难.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
10. 一带电粒子在电场中仅受电场力运动,其速度随时间变化的图象如图所示,从A点运动到B点所对应的时刻分别为tA、tB,则下列说法正确的是( )
一带电粒子在电场中仅受电场力运动,其速度随时间变化的图象如图所示,从A点运动到B点所对应的时刻分别为tA、tB,则下列说法正确的是( )
 一带电粒子在电场中仅受电场力运动,其速度随时间变化的图象如图所示,从A点运动到B点所对应的时刻分别为tA、tB,则下列说法正确的是( )
一带电粒子在电场中仅受电场力运动,其速度随时间变化的图象如图所示,从A点运动到B点所对应的时刻分别为tA、tB,则下列说法正确的是( )| A. | B处的电场强度一定小于A处的电场强度 | |
| B. | B处的电势一定低于A处的电势 | |
| C. | 电荷在A处的电势能一定小于B处的电势能 | |
| D. | 电荷在从A到B的过程中,电场力一定对电荷做正功 |
15.以速度v0水平抛出一物体,当其竖直分位移与水平分位移相等时,则下列计算数据错误的是( )
| A. | 瞬时速度为$\sqrt{5}$v0 | B. | 发生的位移为$\frac{2\sqrt{2}{{v}_{0}}^{2}}{g}$ | ||
| C. | 运动时间为$\frac{2{v}_{0}}{g}$ | D. | 竖直分速度等于水平分速度 |
5.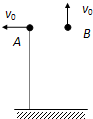 如图所示,两个完全相同的小球A、B,在同一高度处以相同大小的初速度v0分别水平抛出和竖直向上抛出,下列说法正确的是( )
如图所示,两个完全相同的小球A、B,在同一高度处以相同大小的初速度v0分别水平抛出和竖直向上抛出,下列说法正确的是( )
 如图所示,两个完全相同的小球A、B,在同一高度处以相同大小的初速度v0分别水平抛出和竖直向上抛出,下列说法正确的是( )
如图所示,两个完全相同的小球A、B,在同一高度处以相同大小的初速度v0分别水平抛出和竖直向上抛出,下列说法正确的是( )| A. | 两小球落地时的速度相同 | |
| B. | 两小球落地时,重力的瞬时功率相同 | |
| C. | 从开始运动至落地,重力势能变化相同 | |
| D. | 从开始运动至落地,重力对两小球做功的平均功率相同 |
12.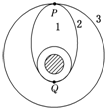 卫星的发射往往不是“一步到位”,而是经过几次变轨才定位在圆周轨道上的.神舟七号飞船发射升空后,先在近地点高度200公里、远地点高度347公里的椭圆轨道上运行5圈,当飞船在远地点时实施变轨进入347公里的圆轨道.飞船变轨过程可简化为如图所示,假设在椭圆轨道2的P点为椭圆轨道2进入圆轨道3的相切点,则( )
卫星的发射往往不是“一步到位”,而是经过几次变轨才定位在圆周轨道上的.神舟七号飞船发射升空后,先在近地点高度200公里、远地点高度347公里的椭圆轨道上运行5圈,当飞船在远地点时实施变轨进入347公里的圆轨道.飞船变轨过程可简化为如图所示,假设在椭圆轨道2的P点为椭圆轨道2进入圆轨道3的相切点,则( )
 卫星的发射往往不是“一步到位”,而是经过几次变轨才定位在圆周轨道上的.神舟七号飞船发射升空后,先在近地点高度200公里、远地点高度347公里的椭圆轨道上运行5圈,当飞船在远地点时实施变轨进入347公里的圆轨道.飞船变轨过程可简化为如图所示,假设在椭圆轨道2的P点为椭圆轨道2进入圆轨道3的相切点,则( )
卫星的发射往往不是“一步到位”,而是经过几次变轨才定位在圆周轨道上的.神舟七号飞船发射升空后,先在近地点高度200公里、远地点高度347公里的椭圆轨道上运行5圈,当飞船在远地点时实施变轨进入347公里的圆轨道.飞船变轨过程可简化为如图所示,假设在椭圆轨道2的P点为椭圆轨道2进入圆轨道3的相切点,则( )| A. | 在P点需要点火,使飞船加速 | |
| B. | 飞船在轨道2经过P点时的加速度小于它在轨道3上经过P点的加速度 | |
| C. | 飞船在轨道2经过P点时的速度大于它在轨道3上经过P点的速度 | |
| D. | 飞船在轨道2上运动到Q点时的速度小于在轨道3上经过P点的速度 |
9.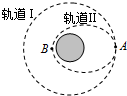 航天飞机在完成对哈勃空间望远镜的维修任务后,在A点短时间开动小型发动机进行变轨,从圆形轨道Ⅰ进入椭圆道Ⅱ,B为轨道Ⅱ上的一点,如图所示,下列说法中正确的是( )
航天飞机在完成对哈勃空间望远镜的维修任务后,在A点短时间开动小型发动机进行变轨,从圆形轨道Ⅰ进入椭圆道Ⅱ,B为轨道Ⅱ上的一点,如图所示,下列说法中正确的是( )
 航天飞机在完成对哈勃空间望远镜的维修任务后,在A点短时间开动小型发动机进行变轨,从圆形轨道Ⅰ进入椭圆道Ⅱ,B为轨道Ⅱ上的一点,如图所示,下列说法中正确的是( )
航天飞机在完成对哈勃空间望远镜的维修任务后,在A点短时间开动小型发动机进行变轨,从圆形轨道Ⅰ进入椭圆道Ⅱ,B为轨道Ⅱ上的一点,如图所示,下列说法中正确的是( )| A. | 在轨道Ⅱ上经过A的速度大于经过B的速度 | |
| B. | 在轨道Ⅱ上经过B的速度大于在轨道I上运动的速度 | |
| C. | 在轨道Ⅱ上运动的周期大于在轨道Ⅰ上运动的周期 | |
| D. | 在轨道Ⅱ上经过A的加速度等于在轨道Ⅰ上经过A的加速度 |
10.当两列水波发生干涉时,如果两列波的波峰在P点相遇,下列说法正确的是( )
| A. | 质点P的振动有时加强,有时减弱 | B. | 质点P的振幅最大 | ||
| C. | 质点P的位移始终最大 | D. | 质点P的位移不会为零 |
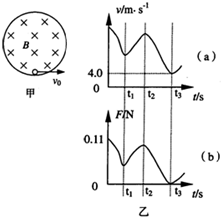 在竖直平面内有一圆形绝缘轨道,半径为R=0.4m,匀强磁场垂直于轨道平面向里,一质量为m=1×10-3kg、带电荷量为q=+3×10-2C的小球,可在内壁滚动,如图甲所示.开始时,在最低点处给小球一个初速度v0,使小球在竖直平面内逆时针做圆周运动,图乙(a)是小球在竖直平面内做圆周运动的速率v随时间t变化的情况,图乙(b)是小球所受轨道的弹力F随时间t变化的情况,结合图象所给数据,(取g=10m/s2).求:
在竖直平面内有一圆形绝缘轨道,半径为R=0.4m,匀强磁场垂直于轨道平面向里,一质量为m=1×10-3kg、带电荷量为q=+3×10-2C的小球,可在内壁滚动,如图甲所示.开始时,在最低点处给小球一个初速度v0,使小球在竖直平面内逆时针做圆周运动,图乙(a)是小球在竖直平面内做圆周运动的速率v随时间t变化的情况,图乙(b)是小球所受轨道的弹力F随时间t变化的情况,结合图象所给数据,(取g=10m/s2).求: