题目内容
4.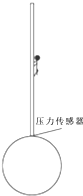 在2012年元旦晚会上,河北杂技团表演了杂技“大球扛杆”.在一个大球上竖立一根直杆,演员在直杆上做了精彩表演.如图所示.假设直杆与大球之间有一压力传感器.一个质量为50kg的演员匀速向上运动时传感器显示压力为600N;演员从直杆最上端由静止开始向下匀加速运动一段时间后又匀减速运动一段时间速度减小到零,静止在距直杆底端$\frac{1}{3}$处.已知在演员向下运动时传感器显示的最大压力为700N,最小压力为500N,直杆长度为12m,g取10m/s2.求:
在2012年元旦晚会上,河北杂技团表演了杂技“大球扛杆”.在一个大球上竖立一根直杆,演员在直杆上做了精彩表演.如图所示.假设直杆与大球之间有一压力传感器.一个质量为50kg的演员匀速向上运动时传感器显示压力为600N;演员从直杆最上端由静止开始向下匀加速运动一段时间后又匀减速运动一段时间速度减小到零,静止在距直杆底端$\frac{1}{3}$处.已知在演员向下运动时传感器显示的最大压力为700N,最小压力为500N,直杆长度为12m,g取10m/s2.求:(1)直杆的质量;
(2)演员下降过程中加速、减速的加速度;
(3)演员向下运动的平均速度.
分析 (1)传感器显示压力等于大球对直杆的支持力.根据演员向上匀速运动时传感器的压力,对演员和直杆整体研究,运用平衡条件求解直杆的质量.
(2)根据牛顿第三定律得到大球对直杆的支持力,再根据演员匀速运动时受力平衡,求得摩擦力,再运用牛顿第二定律分别求解加速、减速运动的加速度.
(3)演员加速和减速两个过程的加速度大小相等,由速度公式求出最大速度,即可求得平均速度
解答 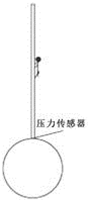 解:(1)设直杆质量为m0,由牛顿第三定律,传感器显示压力等于大球对直杆的支持力.由平衡条件:m0g+mg=F0解得m0=$\frac{{F}_{0}}{g}$-m=10kg.
解:(1)设直杆质量为m0,由牛顿第三定律,传感器显示压力等于大球对直杆的支持力.由平衡条件:m0g+mg=F0解得m0=$\frac{{F}_{0}}{g}$-m=10kg.
(2)设演员向下运动的加速度为a,由牛顿第三定律,传感器显示的最大压力F1=700N等于大球对直杆的最大支持力,对直杆,由平衡条件得演员到直杆向下的摩擦力f1=F1-m0g=600N
由牛顿第三定律,直杆对演员向上的摩擦力等于600N
对演员,由牛顿第二定律:f1-mg=ma1
解得匀减速向下运动的加速度大小为a1=2m/s2
由牛顿第三定律,传感器显示的最小压力F2=500N等于大球对直杆的最小支持力
对直杆,由平衡条件得演员对直杆向下的摩擦力f2=F2-m0g=400N
由牛顿第三定律,直杆对演员向上的摩擦力等于400N
对演员,由牛顿第二定律:mg-f2=ma2
解得匀加速向下运动的加速度大小为a2=2m/s2
演员下降过程中加速、减速的加速度大小均为2m/s2,方向相反.
(3)由第(2)问知演员匀加速运动和匀减速运动加速度大小相等,设演员加速运动时间为t,由题述可知
4=$\frac{1}{2}$at2,解得t=2s
演员向下运动的最大速度vm=at=4m/s
演员向下运动的平均速度v=$\frac{{v}_{m}}{2}$=2m/s.
答:
(1)直杆的质量为10kg;
(2)演员下降过程中加速、减速的加速度大小均为2m/s2,方向相反.
(3)演员向下运动的平均速度为2m/s
点评 本题涉及的过程较多,分析受力情况是关键,运用牛顿第二定律和运动学公式求解,对于平均速度也可以根据位移与时间之比求解

| A. | 库仑首先提出用电场线描绘抽象的电场这种形象化的研究方法 | |
| B. | 牛顿首次提出“提出假说,数学推理,实验验证,合理外推”的科学推理方法 | |
| C. | 用质点来代替有质量的物体是采用了理想模型的方法 | |
| D. | 场强表达式E=$\frac{F}{q}$和加速度表达式a=$\frac{F}{m}$都是利用比值法得到的定义式 |
| A. | 带电体的线度足够小 | |
| B. | 带电体的长度与它到场点的距离相比足够小 | |
| C. | 带电体所带的电量足够小 | |
| D. | 带电体的线度及带电量都足够小 |
| A. | 汽车机械能守恒 | |
| B. | 汽车的动能和势能相互转化 | |
| C. | 汽车的机械能转化为内能,总能量减少 | |
| D. | 机械能逐渐转化为内能,总能量守恒 |
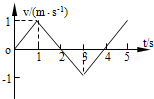
| A. | 第1s内和第2s内的速度方向相反 | B. | 第2s内的速度和加速度方向相反 | ||
| C. | 前 4s内质点的位移为零 | D. | 第3s末和第5s末质点的位置相同 |

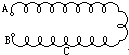 如图,一圈粗细均匀的导线长s,在两端点A、B间加上恒定电压时,测得通过导线的电流为IA,如剪去BC段,在A、C两端加同样电压时,通过导线的电流变为IB,则剪去的BC段多长?
如图,一圈粗细均匀的导线长s,在两端点A、B间加上恒定电压时,测得通过导线的电流为IA,如剪去BC段,在A、C两端加同样电压时,通过导线的电流变为IB,则剪去的BC段多长?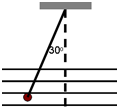 一个质量m=30g,带电荷量为q=-2×10-8C的半径极小的小球,用丝线悬挂在某匀强电场中,电场线水平.当小球静止时,测得悬线与竖直方向成30°夹角,如图所示,求该电场的场强大小,并说明场强方向.
一个质量m=30g,带电荷量为q=-2×10-8C的半径极小的小球,用丝线悬挂在某匀强电场中,电场线水平.当小球静止时,测得悬线与竖直方向成30°夹角,如图所示,求该电场的场强大小,并说明场强方向.