题目内容
13.A、B两列火车在同一轨道上同向行驶,A车在前,其速度vA=10m/s,B车在后,其速度为vB=30m/s.因大雾能见度低,B车在距A车90m时,才发现前方有A车,反应0.5s后,B车立即刹车,假设B车刹车过程可以看作匀减速直线运动,试计算B车要不撞上A车,刹车的加速度最少是多大?分析 B车不撞上A车的临界情况是速度相等时,恰好不相撞,结合位移关系,根据运动学公式求出刹车的最小加速度.
解答 解:B车在反应时间内的位移为:
xB1=vB△t=30×0.5m=15m,
两车速度相等经历的时间为:
$t=\frac{{v}_{A}-{v}_{B}}{a}=\frac{-20}{a}$,
B车的位移为:${x}_{B}={x}_{B1}+\frac{{{v}_{A}}^{2}-{{v}_{B}}^{2}}{2a}$,
A车的位移为:xA=vAt,
恰好不相撞的临界情况是:xB=xA+90m,
代入数据联立解得:a=$-\frac{8}{3}m/{s}^{2}$.
答:刹车的加速度最少是$-\frac{8}{3}m/{s}^{2}$.
点评 本题考查了运动学中的临界问题,关键抓住临界情况,即速度相等时,恰好不相撞,结合位移关系进行求解,难度中等.

练习册系列答案
相关题目
3.沿直线做匀变速运动的一列火车和一辆汽车的速度分别为v1和v2,v1、v2在各个时刻的大小如表所示,从表中数据可以看出( )
| t/s | 0 | 1 | 2 | 3 | 4 |
| v1/m•s-1 | 18.0 | 17.5 | 17.0 | 16.5 | 16.0 |
| v2/m•s-1 | 9.8 | 11.0 | 12.2 | 13.4 | 14.6 |
| A. | 火车的速度变化较慢 | B. | 汽车的加速度较小 | ||
| C. | 火车的位移在减小 | D. | 汽车的位移在增加 |
4.真空中有一个电场,在这个电场中的某一点放入电量为3.2×10-7C的点电荷,它受到的电场力为3.2×10-4N,那么这一点处的电场强度的大小等于( )
| A. | 600N/C | B. | 800N/C | C. | 1000N/C | D. | 1800N/C |
1.汽车由静止开始先以加速度a1做匀加速直线运动,一段时间后立即刹车,刹车的加速度大小为a2,直至停止,运动的总时间为t,则加速的时间是( )
| A. | $\frac{{a}_{1}}{{a}_{2}}t$ | B. | $\frac{{a}_{2}}{{a}_{1}}t$ | C. | $\frac{{a}_{1}}{{a}_{1}+{a}_{2}}t$ | D. | $\frac{{a}_{2}}{{a}_{1}+{a}_{2}}t$ |
8.关于电场强度,下述说法正确的是( )
| A. | 根据E=$\frac{F}{q}$,可知电场中某点的场强由试探电荷受到电场力及其电量共同决定 | |
| B. | 根据E=$\frac{KQ}{{r}^{2}}$,可知点电荷电场中某点的场强大小与该点到点电荷距离的二次方成反比 | |
| C. | 根据E=$\frac{U}{d}$,可知匀强电场中的场强在数值上等于单位距离上的电势差 | |
| D. | 电场强度是矢量,其方向跟试探电荷在该点的受力方向相同 |
18.关于加速度,下列说法正确的是( )
| A. | 加速度就是速度的增加量 | |
| B. | 加速度可能是速度的减小量 | |
| C. | 加速度为正值则说明物体一定在做加速运动 | |
| D. | 加速度大说明物体速度的变化率大 |
2. 如图所示是显微镜下观察水中悬浮的花粉颗粒时,对其中三个颗粒每隔30s记录观察到的位置,再用直线把它们依次连接起来而成,由图可判断( )
如图所示是显微镜下观察水中悬浮的花粉颗粒时,对其中三个颗粒每隔30s记录观察到的位置,再用直线把它们依次连接起来而成,由图可判断( )
 如图所示是显微镜下观察水中悬浮的花粉颗粒时,对其中三个颗粒每隔30s记录观察到的位置,再用直线把它们依次连接起来而成,由图可判断( )
如图所示是显微镜下观察水中悬浮的花粉颗粒时,对其中三个颗粒每隔30s记录观察到的位置,再用直线把它们依次连接起来而成,由图可判断( )| A. | 水分子的运动轨迹 | B. | 花粉颗粒的运动轨迹 | ||
| C. | 水分子作无规则运动 | D. | 花粉颗粒有时不运动 |
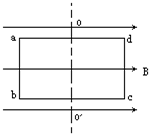 如图所示,闭合的单匝线圈放在匀强磁场中,以角速度ω=300弧度/秒绕中心轴oo′逆时针匀速转动(沿oo′方向看).oo′轴垂直磁场方向.线圈的ab边长为0.1米,bc边长为0.2米,线圈的总电阻R=0.05欧,B=0.5特.从中性面开始转动,求:
如图所示,闭合的单匝线圈放在匀强磁场中,以角速度ω=300弧度/秒绕中心轴oo′逆时针匀速转动(沿oo′方向看).oo′轴垂直磁场方向.线圈的ab边长为0.1米,bc边长为0.2米,线圈的总电阻R=0.05欧,B=0.5特.从中性面开始转动,求: