题目内容
18. 如图所示,质量为m的质点在水平面上受到同一水平面上三个恒力F1、F2、F3的作用而做匀速直线运动,速度v的方向与恒力F2的方向相同.只把恒力F2在水平面内沿逆时针方向瞬间转过90°后(F2的大小不变)( )
如图所示,质量为m的质点在水平面上受到同一水平面上三个恒力F1、F2、F3的作用而做匀速直线运动,速度v的方向与恒力F2的方向相同.只把恒力F2在水平面内沿逆时针方向瞬间转过90°后(F2的大小不变)( )| A. | 质点仍以速度做匀速直线运动 | |
| B. | 质点将以速率做匀速圆周运动 | |
| C. | 质点将以加速度a=$\frac{{F}_{2}}{m}$做匀变速曲线运动 | |
| D. | 质点将以加速度a=$\frac{\sqrt{2}{F}_{2}}{m}$做匀变速曲线运动 |
分析 当物体受到的合外力恒定时,若物体受到的合力与初速度不共线时,物体做曲线运动;若合力与初速度共线,物体做直线运动.
根据牛顿第二定律求出加速度.
解答 解:物体在F1、F2、F3三个共点力作用下做匀速直线运动,三力平衡,必有F1与F3、F2的合力等大反向,当F2大小不变,方向改变90°时,F3、F1的合力大小仍为F2,方向与改变方向后的F2夹角为90°,故F合=$\sqrt{2}$F2,物体做匀变速运动,
由于速度v的方向与恒力F2改变前的方向相同,故此时F合方向与速度方向夹角为135度,物体做匀变速曲线运动.
根据牛顿第二定律得:a=$\frac{{F}_{合}}{m}$=$\frac{\sqrt{2}{F}_{2}}{m}$,故ABC错误,D正确;
故选:D.
点评 本题关键先根据平衡条件得出力F1变向后的合力大小和方向,根据曲线运动的条件判断物体的运动性质,根据力与初速度夹角为任何值都有可能得知力可能做正功也可能做负功.

练习册系列答案
相关题目
8. 如图所示,一个劈形物体A,各面均光滑,放在固定的斜面上,上表面呈水平,在水平面上放一个小球B,劈形物体从静止开始释放,则小球在碰到斜面前的运动轨迹是( )
如图所示,一个劈形物体A,各面均光滑,放在固定的斜面上,上表面呈水平,在水平面上放一个小球B,劈形物体从静止开始释放,则小球在碰到斜面前的运动轨迹是( )
 如图所示,一个劈形物体A,各面均光滑,放在固定的斜面上,上表面呈水平,在水平面上放一个小球B,劈形物体从静止开始释放,则小球在碰到斜面前的运动轨迹是( )
如图所示,一个劈形物体A,各面均光滑,放在固定的斜面上,上表面呈水平,在水平面上放一个小球B,劈形物体从静止开始释放,则小球在碰到斜面前的运动轨迹是( )| A. | 沿斜面向下的直线 | B. | 竖直向下的直线 | ||
| C. | 无规则曲线 | D. | 抛物线 |
9.一个物体以v0=16m/s的初速度冲上一光滑斜面,加速度的大小为8m/s2,冲上最高点之后,又以相同的加速度往回运动.则( )
| A. | 1 s末的速度大小为8 m/s | B. | 3 s末的速度为零 | ||
| C. | 2 s内的位移大小是16 m | D. | 3 s内的位移大小是12 m |
3. 如图所示,小车的质量为M.人的质量为m,人用恒力F拉绳,若人和车保持相对静止.不计绳和滑轮质量、车与地面的摩擦,则车对人的摩擦力可能是( )
如图所示,小车的质量为M.人的质量为m,人用恒力F拉绳,若人和车保持相对静止.不计绳和滑轮质量、车与地面的摩擦,则车对人的摩擦力可能是( )
 如图所示,小车的质量为M.人的质量为m,人用恒力F拉绳,若人和车保持相对静止.不计绳和滑轮质量、车与地面的摩擦,则车对人的摩擦力可能是( )
如图所示,小车的质量为M.人的质量为m,人用恒力F拉绳,若人和车保持相对静止.不计绳和滑轮质量、车与地面的摩擦,则车对人的摩擦力可能是( )| A. | 若M=m,则摩擦力为0 | B. | 若M=m,则摩擦力方向向右 | ||
| C. | 若M<m,则摩擦力方向向右 | D. | 若M>m,则摩擦力方向向右 |
7. A、B两物体同时由同一地点向同一方向作 直线运动,其υ-t图象如图所示,下列说法正确的是( )
A、B两物体同时由同一地点向同一方向作 直线运动,其υ-t图象如图所示,下列说法正确的是( )
 A、B两物体同时由同一地点向同一方向作 直线运动,其υ-t图象如图所示,下列说法正确的是( )
A、B两物体同时由同一地点向同一方向作 直线运动,其υ-t图象如图所示,下列说法正确的是( )| A. | 20~40s内A、B两物体间的距离逐渐减小 | |
| B. | 0~20s内A、B两物体间的距离逐渐减小 | |
| C. | B物体的加速度为0.5m/s2 | |
| D. | 在第20s末两物体相遇 |
3.下列关于功的说法正确的是( )
| A. | 力是矢量,位移是矢量,所以功也是矢量 | |
| B. | 功有正、负之分,所以正功大于负功 | |
| C. | 若某一个力对物体不做功,说明该物体一定没有运动 | |
| D. | 力对物体做的功等于这个力的大小、物体位移大小及力和位移间夹角的余弦三者的乘积 |

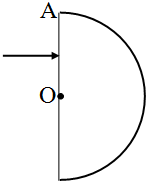 圆柱透镜的截面如图所示,圆心为O,半径OA=R,一束光从半径OA的中点垂直于界面射入透镜后,从圆弧面射出,出射光线相对入射光线偏折了15°角,求透镜的折射率.要使这束光线不能从圆弧面射出,可使透镜从图示位置沿垂直于入射光线方向平移多少?向上平移还是向下平移?
圆柱透镜的截面如图所示,圆心为O,半径OA=R,一束光从半径OA的中点垂直于界面射入透镜后,从圆弧面射出,出射光线相对入射光线偏折了15°角,求透镜的折射率.要使这束光线不能从圆弧面射出,可使透镜从图示位置沿垂直于入射光线方向平移多少?向上平移还是向下平移? 某同学尝试用橡皮筋等器材验证力的平行四边形定则,他找到两条相同的橡皮筋(遵循胡克定律)和若干小重物,以及刻度尺、三角板、铅笔、细绳、白纸、钉子,设计了如下实验:将两条橡皮筋的一端与细绳连接,结点为O,细绳下挂一重物,两橡皮筋的另一端也都连有细绳.实验时,先将一条橡皮筋的另一端的细绳固定在墙上的钉子A上,另一条橡皮筋任其下垂,如图1所示;再将另一条橡皮筋的另一端的细绳也固定在墙上的钉子B上,如图2所示.
某同学尝试用橡皮筋等器材验证力的平行四边形定则,他找到两条相同的橡皮筋(遵循胡克定律)和若干小重物,以及刻度尺、三角板、铅笔、细绳、白纸、钉子,设计了如下实验:将两条橡皮筋的一端与细绳连接,结点为O,细绳下挂一重物,两橡皮筋的另一端也都连有细绳.实验时,先将一条橡皮筋的另一端的细绳固定在墙上的钉子A上,另一条橡皮筋任其下垂,如图1所示;再将另一条橡皮筋的另一端的细绳也固定在墙上的钉子B上,如图2所示.