题目内容
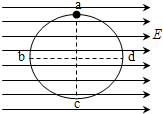 一半径为R的光滑圆环竖直放在水平向右的场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动,已知小球自a点由静止释放,沿abc运动到d点时速度恰好为零,由此可知( )
一半径为R的光滑圆环竖直放在水平向右的场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动,已知小球自a点由静止释放,沿abc运动到d点时速度恰好为零,由此可知( )①.小球所受重力与电场力大小相等
②.小球在b点时的机械能最小
③.小球在d点时的电势能最大
④.小球在c点时的动能最大.
分析:由题,小球自a点由静止释放,沿abc运动到d点时速度恰好为零,由动能定理可求出重力与电场力的关系,并且可知小球带负电,电场力做负功.分别分析小球从a到b、d、c时,电场力做功情况,可判断机械能、电势能的大小,由重力和电场力做的总功情况可分析动能的大小.
解答:解:①小球a→b→c→d的过程中,由动能定理得:mgR-FR=0,得,电场力F=mg,并可知,小球带负电.故①正确.
②小球从a→b→c→d的过程中,a→b过程中,电场力做正功,而且最大,则小球b点的机械能最大.故②错误.
③a→d过程中,电场力做负功,而且最大,则小球d点的电势能最大.故③正确.
④小球从a→c过程中,到达bc中点时,电场力和重力的合力所做的总功最大,所以小球到达bc中点时动能都最大.故④错误.
故选D
②小球从a→b→c→d的过程中,a→b过程中,电场力做正功,而且最大,则小球b点的机械能最大.故②错误.
③a→d过程中,电场力做负功,而且最大,则小球d点的电势能最大.故③正确.
④小球从a→c过程中,到达bc中点时,电场力和重力的合力所做的总功最大,所以小球到达bc中点时动能都最大.故④错误.
故选D
点评:本题运用动能定理分析小球的各种能量的变化,掌握了各种能与功的对应关系,就能正确解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一半径为R的光滑圆环竖直放在水平向右的场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动,已知小球自a点由静止释放,沿abc运动到d点时速度恰好为零,由此可知( )
一半径为R的光滑圆环竖直放在水平向右的场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动,已知小球自a点由静止释放,沿abc运动到d点时速度恰好为零,由此可知( )| A、小球所受重力与电场力大小相等 | B、小球在b点时的机械能最小 | C、小球在d点时的电势能最大 | D、小球在c点时的动能最大 |
 一半径为R的光滑圆环竖直放在水平向右的场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动,已知小球自a点由静止释放,沿abc运动到d点时速度恰好为零,由此可知( )
一半径为R的光滑圆环竖直放在水平向右的场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动,已知小球自a点由静止释放,沿abc运动到d点时速度恰好为零,由此可知( ) (2009?安庆三模)在竖直平面内有一半径为R的光滑圆环轨道,一质量为m的小球穿在圆环轨道上做圆周运动,到达最高点C时的速率vc=
(2009?安庆三模)在竖直平面内有一半径为R的光滑圆环轨道,一质量为m的小球穿在圆环轨道上做圆周运动,到达最高点C时的速率vc=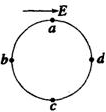 一半径为R的光滑圆环竖直放在水平向右场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动.现使小球由a点静止释放,沿abc运动到d点时速度恰好为零,由此可知,小球在b点时( )
一半径为R的光滑圆环竖直放在水平向右场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动.现使小球由a点静止释放,沿abc运动到d点时速度恰好为零,由此可知,小球在b点时( )