题目内容
静止的氡核(
Rn)放出一个速度为v0的α粒子,若衰变过程中释放的核能全部转化为α粒子及反冲核的动能,已知原子质量单位为u,真空中的光速为c,试求在衰变过程中的质量亏损.(不计相对论修正,在涉及动量问题时,亏损的质量可忽略不计.)
222 86 |
分析:先根据动量守恒定律列方程求解出α衰变后新核的速度;然后根据爱因斯坦质能方程求解质量亏损.
解答:解:设α粒子的质量为m1,氡核的质量为m2,反冲核的速度大小为v.
则根据动量守恒定律可得:m1v0=(m2-m1)v ①
由题意得,释放的核能E=
m1
+
(m2-m1)v2 ②
由质能方程得:E=△mc2 ③
联立以上三式解得:△m=
答:在衰变过程中的质量亏损为
.
则根据动量守恒定律可得:m1v0=(m2-m1)v ①
由题意得,释放的核能E=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
由质能方程得:E=△mc2 ③
联立以上三式解得:△m=
222u
| ||
| 109c2 |
答:在衰变过程中的质量亏损为
222u
| ||
| 109c2 |
点评:本题关键根据动量守恒定律求解反应后新核的速度,然后根据质能方程列式求解质量亏损;要注意在涉及动量问题时,亏损的质量可忽略不计.

练习册系列答案
相关题目
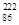 Rn,放出一个α粒子后衰变为钋核
Rn,放出一个α粒子后衰变为钋核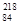 Po,同时放出能量为E=0.26 MeV的光子.假设放出的核能完全转变为钋核与α粒子的动能,不计光子的动量.已知M氡=222.08663 u、mα=4.0026 u、M钋=218.0766 u,1 u相当于931.5 MeV的能量.
Po,同时放出能量为E=0.26 MeV的光子.假设放出的核能完全转变为钋核与α粒子的动能,不计光子的动量.已知M氡=222.08663 u、mα=4.0026 u、M钋=218.0766 u,1 u相当于931.5 MeV的能量.