��Ŀ����
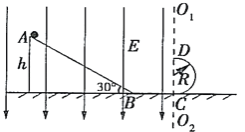
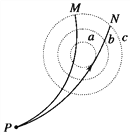
����Ŀ����ͼ����ʾ�����ݿ���Բ��������ת�������䣬����������ʩ����ħ��һ��������Ϊ��ħ���������� ���ɵ�ЧΪһ�ʵ���Բ�������˶�ģ�ͣ���ͼ����ʾ������ֱƽ���ڹ̶���ǿ����Բ����뾶ΪR��A��B����ֱ�Ϊ�������ߵ�����͵㡣�ʵ��ع�������������Բ���˶�����Բ�����ǿ��������ʼ��ָ��Բ��O�Ҵ�С��ΪF�����ʵ�������![]() ͨ��A��ʱ���Թ����ѹ��Ϊ��������8��������Ħ���Ϳ����������ʵ�����Ϊm���������ٶ�Ϊg����
ͨ��A��ʱ���Թ����ѹ��Ϊ��������8��������Ħ���Ϳ����������ʵ�����Ϊm���������ٶ�Ϊg����

A. ǿ���������Ĵ�С![]()
B. �ʵ���A��Թ����ѹ��С����B��Թ����ѹ��
C. ֻҪ�ʵ�����������Բ���˶������ʵ��A��B.�����ѹ�����Ϊ![]()
D. ������������С��Ϊ2F��Ϊȷ���ʵ���������Բ���˶������ʵ�ͨ��B����������Ϊ![]()
���𰸡�D
��������
A.��A�㣬���ʵ㣬��ţ�ٵڶ������У�
![]()
����ţ�ٵ��������У�
FA��FA�䣽8mg
������ã�
F��8mg
��A����.
BC.�ʵ������Բ���˶�����A�㣺����ţ�ٵڶ������У�
![]()
����ţ�ٵ��������У�
NA��NA��
��B�㣬����ţ�ٵڶ������У�
![]()
����ţ�ٵ��������У�NB��NB��
��A�㵽B����̣����ݻ�е���غ㶨���У�
![]()
������ã�
NA�䩁NB�䣽6mg
��BC����.
D��������������С��Ϊ2F����B�㣬����ţ�ٵڶ����ɣ�
![]()
��FB��0���ʵ��ٶ����vB��vBm
![]()
������ã�
![]()
��D��ȷ.

 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�