题目内容
19.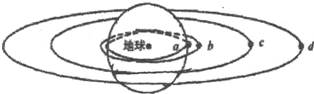 有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )
有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )| A. | a的向心加速度等于重力加速度g | B. | 在相同时间内b转过的弧长最长 | ||
| C. | C离地高度可以是任意值 | D. | d运动的周期最长 |
分析 根据万有引力提供向心力得出线速度、周期的表达式,从而比较出大小,得出相同时间内转过的弧长,同步卫星定轨道、定高度、定周期、定速率.
解答 解:A、卫星a在赤道平面随地球一起转动,靠万有引力和支持力的合力提供向心力,不是靠重力提供向心力,所以a的向心加速度不等于重力加速度g,故A错误.
B、根据$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=mr\frac{4{π}^{2}}{{T}^{2}}$得,v=$\sqrt{\frac{GM}{r}}$,$T=\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$,a、c的角速度相同,c的半径大,则c的线速度大于a的线速度,b、c、d中,b的线速度最大,可知b的线速度最大,相同时间内弧长最长.d的轨道半径最大,则周期最长,故B、D正确.
C、c为同步卫星,轨道半径一定,则高度一定,故C错误.
故选:BD.
点评 解决本题的关键知道线速度、角速度、周期、向心加速度与轨道半径的大小关系,以及知道同步卫星的特点,难度中等.

练习册系列答案
相关题目
9. 有一些问题你可能不会求解,但是你仍有可能对这些问题的解是否合理进行分析和判断,例如从解得物理量单位,解随某些已知量变化的趋势,解在一种特殊条件下的结果等方面进行分析,并与预期结果,实验结论等进行比较,从而判断解的合理性或正确性.
有一些问题你可能不会求解,但是你仍有可能对这些问题的解是否合理进行分析和判断,例如从解得物理量单位,解随某些已知量变化的趋势,解在一种特殊条件下的结果等方面进行分析,并与预期结果,实验结论等进行比较,从而判断解的合理性或正确性.
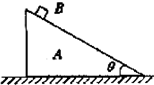
举例如下:如图所示.质量为M,倾角为θ的滑块A放于水平地面上,把质量为m的滑块B放在A的斜面上.忽略一切摩擦,有人求得B相对地面的加速度a=$\frac{M+m}{M+m{sin}^{2}θ}$gsinθ,式中g为重力加速度.对于上述解,某同学首先分析了等号右侧量的单位,没发现问题.他进一步利用特殊条件对该解做了如下四项分析和判断,所得结论都是“解可能是对的”.但是,其中有一项是错误的.请你指出该项.( )
 有一些问题你可能不会求解,但是你仍有可能对这些问题的解是否合理进行分析和判断,例如从解得物理量单位,解随某些已知量变化的趋势,解在一种特殊条件下的结果等方面进行分析,并与预期结果,实验结论等进行比较,从而判断解的合理性或正确性.
有一些问题你可能不会求解,但是你仍有可能对这些问题的解是否合理进行分析和判断,例如从解得物理量单位,解随某些已知量变化的趋势,解在一种特殊条件下的结果等方面进行分析,并与预期结果,实验结论等进行比较,从而判断解的合理性或正确性.举例如下:如图所示.质量为M,倾角为θ的滑块A放于水平地面上,把质量为m的滑块B放在A的斜面上.忽略一切摩擦,有人求得B相对地面的加速度a=$\frac{M+m}{M+m{sin}^{2}θ}$gsinθ,式中g为重力加速度.对于上述解,某同学首先分析了等号右侧量的单位,没发现问题.他进一步利用特殊条件对该解做了如下四项分析和判断,所得结论都是“解可能是对的”.但是,其中有一项是错误的.请你指出该项.( )
| A. | 当θ°=0时,该解给出a=0,这符合常识,说明该解可能是对的 | |
| B. | 当θ=90°时,该解给出a=g,这符合实验结论,说明该解可能是对的 | |
| C. | 当M>>m时,该解给出a≈$\frac{g}{sinθ}$,这符合预期的结果,说明该解可能是对的 | |
| D. | 当m>>M时,该解给出a≈gsinθ,这符合预期的结果,说明该解可能是对的 |
10.关于伽俐略对自由落体运动的研究,下列哪个过程是他的探究过程( )
| A. | 猜想--问题--数学推理--实验验证--合理外推--得出结论 | |
| B. | 猜想--问题--实验验证--数学推理--合理外推--得出结论 | |
| C. | 问题--猜想--实验验证--数学推理--合理外推--得出结论 | |
| D. | 问题--猜想--数学推理--实验验证--合理外推--得出结论 |
7.小明玩颠乒乓球的游戏,设乒乓球弹起后做竖直上抛运动,每次弹起的高度均为0.2m(忽略空气阻力、球与球拍的接触时间,重力加速度取g=10m/s2),则( )
| A. | 上升阶段中,乒乓球加速度的方向竖直向上 | |
| B. | 乒乓球上升到最高点时,其加速度大小为零 | |
| C. | 乒乓球两次弹起之间的时间间隔为0.2s | |
| D. | 小明每分钟最多颠球150次 |
14.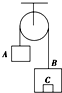 如图所示,质量为m1=2kg的物体A经跨过定滑轮的轻绳与质量为M=5kg的箱子B相连,箱子底板上放一质量为m2=1kg的物体C,不计定滑轮的质量和一切阻力(绳子足够长),在箱子加速下落的过程中,取g=10m/s2,下列正确的是( )
如图所示,质量为m1=2kg的物体A经跨过定滑轮的轻绳与质量为M=5kg的箱子B相连,箱子底板上放一质量为m2=1kg的物体C,不计定滑轮的质量和一切阻力(绳子足够长),在箱子加速下落的过程中,取g=10m/s2,下列正确的是( )
 如图所示,质量为m1=2kg的物体A经跨过定滑轮的轻绳与质量为M=5kg的箱子B相连,箱子底板上放一质量为m2=1kg的物体C,不计定滑轮的质量和一切阻力(绳子足够长),在箱子加速下落的过程中,取g=10m/s2,下列正确的是( )
如图所示,质量为m1=2kg的物体A经跨过定滑轮的轻绳与质量为M=5kg的箱子B相连,箱子底板上放一质量为m2=1kg的物体C,不计定滑轮的质量和一切阻力(绳子足够长),在箱子加速下落的过程中,取g=10m/s2,下列正确的是( )| A. | 物体A处于失重状态,加速度大小为10 m/s2 | |
| B. | 物体A处于超重状态,加速度大小为5 m/s2 | |
| C. | 物体C处于失重状态,对箱子的压力大小为5 N | |
| D. | 轻绳对定滑轮的作用力大小为80 N |
4.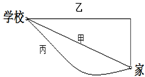 如图,小明从学校出发回家,有三条不同的路可走.关于三条不同的路径,下列说法正确的是( )
如图,小明从学校出发回家,有三条不同的路可走.关于三条不同的路径,下列说法正确的是( )
 如图,小明从学校出发回家,有三条不同的路可走.关于三条不同的路径,下列说法正确的是( )
如图,小明从学校出发回家,有三条不同的路可走.关于三条不同的路径,下列说法正确的是( )| A. | 三条不同的路径对应的路程不同 | |
| B. | 甲通过的路程最大 | |
| C. | 分别走三条不同的路径,位移不同 | |
| D. | 小明从学校到家和从家到校的位移相同 |
8.汉语成语中有一个“形影不离”的成语,意思是人的身体和影子分不开,形容关系密切,经常在一起.在晴天的早上,某同学在操场上跑步,下列说法正确的是( )
①以地面为参考系,影子是静止的
②以地面为参考系,影子是运动的
③以人为参考系,影子是静止的
④以人为参考系,影子是运动的.
①以地面为参考系,影子是静止的
②以地面为参考系,影子是运动的
③以人为参考系,影子是静止的
④以人为参考系,影子是运动的.
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
9. 跨过定滑轮的绳子一端挂一吊板,另一端被吊板上的人拉住,如图,已知人的质量为70kg,吊板质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计.取重力加速度g=10m/s2,当人以440N的力拉绳时,人与吊板的加速度a与人对吊板的压力F分别是( )
跨过定滑轮的绳子一端挂一吊板,另一端被吊板上的人拉住,如图,已知人的质量为70kg,吊板质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计.取重力加速度g=10m/s2,当人以440N的力拉绳时,人与吊板的加速度a与人对吊板的压力F分别是( )
 跨过定滑轮的绳子一端挂一吊板,另一端被吊板上的人拉住,如图,已知人的质量为70kg,吊板质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计.取重力加速度g=10m/s2,当人以440N的力拉绳时,人与吊板的加速度a与人对吊板的压力F分别是( )
跨过定滑轮的绳子一端挂一吊板,另一端被吊板上的人拉住,如图,已知人的质量为70kg,吊板质量为10kg,绳及定滑轮的质量、滑轮的摩擦均可不计.取重力加速度g=10m/s2,当人以440N的力拉绳时,人与吊板的加速度a与人对吊板的压力F分别是( )| A. | a=3m/s2,F=110N | B. | a=3m/s2,F=50N | C. | a=1m/s2,F=260N | D. | a=1m/s2,F=330N |
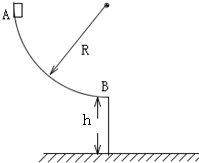 如图所示,半径R=2m的四分之一粗糙的圆弧轨道AB于竖直平面内,轨道B端切线水平,且距水平地面的高度h=1.25m.现将一质量m=0.2kg的小球(可视为质点)从A点由静止释放,小滑块沿圆轨道运动至B点以v=5m/s的速度抛出(g=10m/s2),求:
如图所示,半径R=2m的四分之一粗糙的圆弧轨道AB于竖直平面内,轨道B端切线水平,且距水平地面的高度h=1.25m.现将一质量m=0.2kg的小球(可视为质点)从A点由静止释放,小滑块沿圆轨道运动至B点以v=5m/s的速度抛出(g=10m/s2),求: