题目内容
12.在真空中存在空间足够大的、水平向右的匀强磁场.若将一个质量为m、带正电电量q的小球在此电场中由静止释放,小球将沿与竖直方向夹角为53°的直线运动.现将该小球从电场中某点以初速度v0竖直向上抛出,求运动过程中(sin53°=0.8)(1)此电场的电场强度大小;
(2)小球运动的抛出点至最高点之间的电势差U.
分析 (1)小球在此电场中由静止释放,小球将沿与竖直方向夹角为53°的直线运动,可知重力与电场力的关系,用几何关系求解
(2)电势差U=Ed,其中d为沿电场方向的距离,小球抛出后,由运动的分解知识可知,水平方向做匀加速直线运动,竖直方向做匀减速运动,由运动学方程求解即可
解答 解:(1)小球受重力与电场力作用,由题意得电场力水平向右,且有:
Eq=mgtan53°…①
所以,Eq=$\frac{4}{3}$mg…②
解得E=$\frac{4mg}{3q}$
(2)小球抛出后,竖直方向匀减速运动,由于此方向仅受重力,加速度大小为g,设运动至最高点过程时间为t,则有:
v0=gt…③
水平方向做匀加速运动,此方向仅受电场力,加速度为:
a=$\frac{Eq}{m}$=$\frac{4}{3}$g…④
设运动至最高点过程水平分向位移为d,则:
d=$\frac{1}{2}$at2…⑤
由匀强电场电势差与场强关系得,抛出点至最高点之间的电势差:
U=Ed…⑥
由②③④⑤⑥得:U=$\frac{8m{v}_{0}^{2}}{9q}$
答:(1)电场力水平向右,大小为$\frac{4mg}{3q}$
(2)小球运动的抛出点至最高点之间的电势差为$\frac{8m{v}_{0}^{2}}{9q}$.
点评 本题考查带电粒子在电场和重力场中的运动情况;要注意挖掘隐含信息“小球在此电场中由静止释放,小球将沿与竖直方向夹角为53°的直线运动”,以此为突破口,对于曲线运动问题,用运动分解的办法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图所示,轻质弹簧一端固定在水平面上,另一端放置一质量m=lkg的小球,小球此时处于静止状态,现用竖直向上的拉力F作用在小球上,使小球开始向上做匀加速直线运动,经0.2s弹簧刚好恢复到原长,此时小球的速度为1m/s,整个过程弹簧始终在弹性限度内,g取10m/s2.下列说法正确的是( )
如图所示,轻质弹簧一端固定在水平面上,另一端放置一质量m=lkg的小球,小球此时处于静止状态,现用竖直向上的拉力F作用在小球上,使小球开始向上做匀加速直线运动,经0.2s弹簧刚好恢复到原长,此时小球的速度为1m/s,整个过程弹簧始终在弹性限度内,g取10m/s2.下列说法正确的是( )
 如图所示,轻质弹簧一端固定在水平面上,另一端放置一质量m=lkg的小球,小球此时处于静止状态,现用竖直向上的拉力F作用在小球上,使小球开始向上做匀加速直线运动,经0.2s弹簧刚好恢复到原长,此时小球的速度为1m/s,整个过程弹簧始终在弹性限度内,g取10m/s2.下列说法正确的是( )
如图所示,轻质弹簧一端固定在水平面上,另一端放置一质量m=lkg的小球,小球此时处于静止状态,现用竖直向上的拉力F作用在小球上,使小球开始向上做匀加速直线运动,经0.2s弹簧刚好恢复到原长,此时小球的速度为1m/s,整个过程弹簧始终在弹性限度内,g取10m/s2.下列说法正确的是( )| A. | 在0~0.2s内,拉力的最大功率为15W | |
| B. | 弹簧的劲度系数为100N/cm | |
| C. | 在0.2s时撤去外力,则小球在全过程中能上升的最大高度为15cm | |
| D. | 在0~0.2s内,拉力F对小球做的功等于1.5J |
3.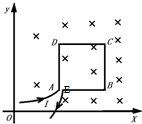 如图所示,在平面直角坐标系的第一象限分布着非匀强磁场,磁场方向垂直纸面向里,沿y轴方向磁场分布是不变的,沿x轴方向磁感应强度与x满足关系B=kx,其中k是一恒定的正数,正方形线框ADCB边长为a,A处有一极小开口AE,由粗细均匀的同种规格导线制成,整个线框放在磁场中,且AD边与y轴平行,AD边与y轴距离为a,线框AE两点与一电源相连,稳定时流入线框的电流为I,关于线框受到的安培力情况,下列说法正确的是( )
如图所示,在平面直角坐标系的第一象限分布着非匀强磁场,磁场方向垂直纸面向里,沿y轴方向磁场分布是不变的,沿x轴方向磁感应强度与x满足关系B=kx,其中k是一恒定的正数,正方形线框ADCB边长为a,A处有一极小开口AE,由粗细均匀的同种规格导线制成,整个线框放在磁场中,且AD边与y轴平行,AD边与y轴距离为a,线框AE两点与一电源相连,稳定时流入线框的电流为I,关于线框受到的安培力情况,下列说法正确的是( )
 如图所示,在平面直角坐标系的第一象限分布着非匀强磁场,磁场方向垂直纸面向里,沿y轴方向磁场分布是不变的,沿x轴方向磁感应强度与x满足关系B=kx,其中k是一恒定的正数,正方形线框ADCB边长为a,A处有一极小开口AE,由粗细均匀的同种规格导线制成,整个线框放在磁场中,且AD边与y轴平行,AD边与y轴距离为a,线框AE两点与一电源相连,稳定时流入线框的电流为I,关于线框受到的安培力情况,下列说法正确的是( )
如图所示,在平面直角坐标系的第一象限分布着非匀强磁场,磁场方向垂直纸面向里,沿y轴方向磁场分布是不变的,沿x轴方向磁感应强度与x满足关系B=kx,其中k是一恒定的正数,正方形线框ADCB边长为a,A处有一极小开口AE,由粗细均匀的同种规格导线制成,整个线框放在磁场中,且AD边与y轴平行,AD边与y轴距离为a,线框AE两点与一电源相连,稳定时流入线框的电流为I,关于线框受到的安培力情况,下列说法正确的是( )| A. | 整个线框受到的合力方向与BD连线垂直 | |
| B. | 整个线框沿y轴方向所受合力为0 | |
| C. | 整个线框在x轴方向所受合力为$\frac{1}{4}$ka2I,沿x轴方向 | |
| D. | 整个线框在x轴方向所受合力为$\frac{3}{4}$ka2I,沿x轴方向 |
4.关于电场强度与电势的关系,下面各种说法中正确的是( )
| A. | 电场强度的方向是电势降低最快的方向 | |
| B. | 电场强度大的地方,电势一定高 | |
| C. | 电场强度不变,电势也不变 | |
| D. | 电场强度为零处,电势一定为零 |
1.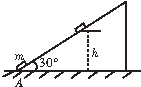 如图所示,一个质量m=1kg的物体,以初谏度v0=8m/s从固定斜面底端冲上倾角a=30°的斜面,到达最高点后返回,已知物体与斜面间的动摩擦因数$μ=\frac{{\sqrt{3}}}{5}$,斜面足够长,取重力加速度g=10m/s2,则下列说法正确的是( )
如图所示,一个质量m=1kg的物体,以初谏度v0=8m/s从固定斜面底端冲上倾角a=30°的斜面,到达最高点后返回,已知物体与斜面间的动摩擦因数$μ=\frac{{\sqrt{3}}}{5}$,斜面足够长,取重力加速度g=10m/s2,则下列说法正确的是( )
 如图所示,一个质量m=1kg的物体,以初谏度v0=8m/s从固定斜面底端冲上倾角a=30°的斜面,到达最高点后返回,已知物体与斜面间的动摩擦因数$μ=\frac{{\sqrt{3}}}{5}$,斜面足够长,取重力加速度g=10m/s2,则下列说法正确的是( )
如图所示,一个质量m=1kg的物体,以初谏度v0=8m/s从固定斜面底端冲上倾角a=30°的斜面,到达最高点后返回,已知物体与斜面间的动摩擦因数$μ=\frac{{\sqrt{3}}}{5}$,斜面足够长,取重力加速度g=10m/s2,则下列说法正确的是( )| A. | 物体上升的最大高度h=2m | |
| B. | 物体上升过程中克服摩擦力做功W=12J | |
| C. | 物体返回A点时重力的功率P=20W | |
| D. | 物体从底端A点开始上滑到返回A点用时t=25s |
2.用水平力F 将木块紧压在紧直墙壁上静止不动,当力F 增加时,木块受到墙对它的支持力N 和摩擦力f 会发生什么样的变化( )
| A. | N增大,f 增大 | B. | N增大,f 不变 | C. | N不变,f 增大 | D. | N不变,f 不变 |