题目内容
3. 如图所示在加速电场正极板附近,一质量为m、带电量为+q的粒子静止释放,加速后沿中轴线射入间距为d,长为L的平行带电金属板A和B.UAB=+U0;测得粒子在AB板间运动时间为t,最后打在靶MN上,不计重力影响,试求:
如图所示在加速电场正极板附近,一质量为m、带电量为+q的粒子静止释放,加速后沿中轴线射入间距为d,长为L的平行带电金属板A和B.UAB=+U0;测得粒子在AB板间运动时间为t,最后打在靶MN上,不计重力影响,试求:(1)加速电压U加的大小;
(2)粒子打在靶MN上的位置到O′点的距离.
分析 (1)粒子在加速电场中加速,在偏转电场中做类平抛运动,应用牛顿第二定律与运动学公式可以求出加速电压.
(2)应用类平抛运动规律可以求出粒子在偏转电场中的偏移量,然后确定打在靶上的位置.
解答 解:(1)粒子在加速电场中,由动能定理得:qU加=$\frac{1}{2}$mv2-0,
粒子在偏转电场中做类平抛运动,在水平方向:L=vt,
解得:U加=$\frac{m{L}^{2}}{2q{t}^{2}}$;
(2)粒子在偏转电场中做类平抛运动,
在竖直方向:y=$\frac{1}{2}$at2=$\frac{1}{2}$$\frac{q{U}_{0}}{md}$$(\frac{L}{v})^{2}$=$\frac{q{U}_{0}{t}^{2}}{2md}$;
答:(1)加速电压U加的大小为$\frac{m{L}^{2}}{2q{t}^{2}}$;
(2)粒子打在靶MN上的位置到O′点的距离为$\frac{q{U}_{0}{t}^{2}}{2md}$.
点评 本题考查了粒子在电场中的运动,分析清楚粒子运动过程,应用动能定理与类平抛运动规律可以解题,本题是一道基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
13.下列物体在运动过程中,机械能守恒的是( )
| A. | 沿斜面减速下滑的物体 | B. | 沿光滑斜面自由下滑的物体 | ||
| C. | 从树上落下的树叶 | D. | 匀速下落的降落伞 |
11.两个分别带有电荷量-Q年+3Q的相同金属小球(均可视为点电荷),固定在相距为r的两处,它们间库仑力的大小为F,两小球相互接触后再分开一定距离,库仑力大小依然为F,则此时两小球相距( )
| A. | 3r | B. | $\frac{1}{3}$r | C. | $\sqrt{3}$r | D. | $\frac{\sqrt{3}}{3}$r |
18. 如图所示,固定在竖直平面内的光滑细杆MN,是按照以初速度v0平抛的运动轨迹制成,M端为抛出点,MN间竖直方向高度差为h.现将一小球套于其上,由静止开始从M端沿杆滑下,已知重力加速度为g,则有( )
如图所示,固定在竖直平面内的光滑细杆MN,是按照以初速度v0平抛的运动轨迹制成,M端为抛出点,MN间竖直方向高度差为h.现将一小球套于其上,由静止开始从M端沿杆滑下,已知重力加速度为g,则有( )
 如图所示,固定在竖直平面内的光滑细杆MN,是按照以初速度v0平抛的运动轨迹制成,M端为抛出点,MN间竖直方向高度差为h.现将一小球套于其上,由静止开始从M端沿杆滑下,已知重力加速度为g,则有( )
如图所示,固定在竖直平面内的光滑细杆MN,是按照以初速度v0平抛的运动轨迹制成,M端为抛出点,MN间竖直方向高度差为h.现将一小球套于其上,由静止开始从M端沿杆滑下,已知重力加速度为g,则有( )| A. | 小球做匀变速曲线运动 | |
| B. | 小球从M端运动到N端所需时间等于$\sqrt{\frac{2h}{g}}$ | |
| C. | 运动到N端时,小球速度的水平分量等于$\frac{{v}_{0}\sqrt{2gh}}{\sqrt{2gh+{{v}_{0}}^{2}}}$ | |
| D. | 运动到N端时,小球速度的竖直分量等于$\sqrt{2gh}$ |
12.如图甲所示,两根间距L=0.4m的平行金属导轨水平放置,导轨的电阻忽略不计,整个装置处于竖直向下的匀强磁场中,磁感应强度B=$\sqrt{2}$T,导轨右端接有一理想变压器,变压器的原、副线圈匝数比为2:1,电表均为理想电表,一根导体棒ab置于导轨上,导体棒电阻不计且始终与导轨良好接触,若导体棒沿平行于导轨的方向在PQ和MN之间运动,其速度图象如图乙的正弦曲线所示,电阻R=10Ω,则下列判断正确的有( )


| A. | 导体棒产生的感应电动势最大值4$\sqrt{2}$V | |
| B. | 交流电压表读数为2V,交流电流表示数为0.2A | |
| C. | 电阻R在1分钟内产生的热量为96J | |
| D. | 增大导体棒运动的频率,其他条件不变,电压表示数将变大 |
13.据新华社报道,由我国自行设计、研制的世界第一套全超导核聚变实验装置(又称“人造太阳”)已完成了首次工程调试.下列关于“人造太阳”的说法中正确的是( )
| A. | “人造太阳”的核反应方程是${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n | |
| B. | “人造太阳”的核反应方程是:${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+3${\;}_{0}^{1}$n | |
| C. | 根据公式△E=△mc2可知,核燃料的质量相同时,聚变反应释放的能量与裂变反应的不能比较大小 | |
| D. | 根据公式E=mc2可知,核燃料的质量相同时,聚变反应释放的能量与裂变反应释放的能量相同 |
 如图所示,一质量为m=2kg的物体,在水平恒力F的作用下,从静止开始运动,已知F=20N,物体与水平面间的动摩擦因数μ=0.5,g=10m/s2,求:
如图所示,一质量为m=2kg的物体,在水平恒力F的作用下,从静止开始运动,已知F=20N,物体与水平面间的动摩擦因数μ=0.5,g=10m/s2,求: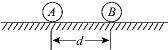 如图:两个带同种电荷的小球A和B,A、B的质量分别为m和2m,开始时将它们固定在绝缘的光滑水平面上保持静止,A、B相距为d,A、B间的相互作用力遵守牛顿第三定律,现同时释放A、B,经过一段时间,B的速度大小为v,A、B间距离为2d.
如图:两个带同种电荷的小球A和B,A、B的质量分别为m和2m,开始时将它们固定在绝缘的光滑水平面上保持静止,A、B相距为d,A、B间的相互作用力遵守牛顿第三定律,现同时释放A、B,经过一段时间,B的速度大小为v,A、B间距离为2d.