题目内容
小军看到打桩机,对打桩机的工作原理产生了兴趣.他构建了一个打桩机的简易模型,如图甲所示.他设想,用恒定大小的拉力F拉动绳端B,使物体从A点(与钉子接触处)由静止开始运动,上升一段高度后撤去F,物体运动到最高点后自由下落并撞击钉子,将钉子打入一定深度.按此模型分析,若物体质量m=1kg,上升1m高度时撤去拉力,撤去拉力前物体的动能Ek与上升高度h的关系图象如图乙所示.(g取10m/s2,不计空气阻力)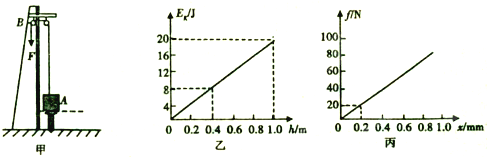
(1)求物体上升到0.4m高度处F的瞬时功率.
(2)若物体撞击钉子后瞬间弹起,且使其不再落下,钉子获得20J的动能向下运动.钉子总长为10cm.撞击前插入部分可以忽略,不计钉子重力.已知钉子在插入过程中所受阻力f与深度x关系图象如图丙所示,求钉子能够陷入的最大深度.

(1)求物体上升到0.4m高度处F的瞬时功率.
(2)若物体撞击钉子后瞬间弹起,且使其不再落下,钉子获得20J的动能向下运动.钉子总长为10cm.撞击前插入部分可以忽略,不计钉子重力.已知钉子在插入过程中所受阻力f与深度x关系图象如图丙所示,求钉子能够陷入的最大深度.
分析:(1)动能与势能之和是物体的机械能,由图2所示图象可以求出物体上升0.4m时物体的速度,根据动能定律求得力F的大小,然后代入功率的计算式即可;
(2)钉子在插入过程中所受阻力f对钉子做功,数值等于钉子动能的改变,根据动能定律即可求得结果.
(2)钉子在插入过程中所受阻力f对钉子做功,数值等于钉子动能的改变,根据动能定律即可求得结果.
解答:解:(1)撤去F前,根据动能定理,有
(F-mg)h=Ek-0
由图象乙得,斜率为k=F-mg=20N,
代入数据解得F=30N,
又由图象得,h=0.4m时,Ek=8J,即v=4m/s
代入数据解得:PF=Fv=120W.
(2)碰撞后,对钉子,有-fx?=0-Ek?
Ek?=20J
f=
又由图象丙得k′=105N/m
代入数据解得:x′=0.02m
答:(1)物体上升到0.4m高度处F的瞬时功率为120W.(2)钉子能够陷入的最大深度为0.02m.
(F-mg)h=Ek-0
由图象乙得,斜率为k=F-mg=20N,
代入数据解得F=30N,
又由图象得,h=0.4m时,Ek=8J,即v=4m/s
代入数据解得:PF=Fv=120W.
(2)碰撞后,对钉子,有-fx?=0-Ek?
Ek?=20J
f=
| k′x′ |
| 2 |
又由图象丙得k′=105N/m
代入数据解得:x′=0.02m
答:(1)物体上升到0.4m高度处F的瞬时功率为120W.(2)钉子能够陷入的最大深度为0.02m.
点评:物体动能与势能之和是物体的机械能,分析清楚图象,应用牛顿第二定律、运动学公式、功率公式等知识即可正确解题.

练习册系列答案
相关题目
 (2013?成都一模)随着中国首艘航母“辽宁号”的下水,同学们对舰载机(图甲)的起降产生了浓厚的兴趣. 下面是小聪编制的一道舰载机降落的题目,请你阅读后求解.
(2013?成都一模)随着中国首艘航母“辽宁号”的下水,同学们对舰载机(图甲)的起降产生了浓厚的兴趣. 下面是小聪编制的一道舰载机降落的题目,请你阅读后求解.
 随着中国首艘航母“辽宁号”的下水,同学们对舰载机(图甲)的起降产生了浓厚的兴趣. 下面是小聪编制的一道舰载机降落的题目,请你阅读后求解.
随着中国首艘航母“辽宁号”的下水,同学们对舰载机(图甲)的起降产生了浓厚的兴趣. 下面是小聪编制的一道舰载机降落的题目,请你阅读后求解. .求该舰载机在航母上滑行时受到的平均阻力. (结果用m、v0;t0表示)
.求该舰载机在航母上滑行时受到的平均阻力. (结果用m、v0;t0表示)