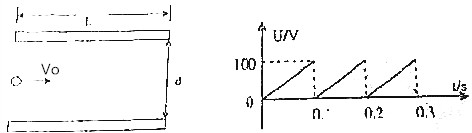题目内容
20.在光滑水平面上有一倾角为37°的光滑斜面,质量为1kg.在斜面上放置一个质量为0.2kg的物体,为使物体与斜面不发生相对滑动,应对施加一个多大的水平力F?方向如何?(g=10m/s2)若斜面粗糙,水平力F为9N时,物体与斜面仍保持相对静止,请分析此时物体受到的摩擦力.
若斜面粗糙,水平力F为12N时,物体与斜面仍保持相对静止,请分析此时物体受到的摩擦力.
若斜面粗糙,水平力F为6N时,物体与斜面仍保持相对静止,请分析此时物体受到的摩擦力.
分析 对物体受力分析,重力支持力,由牛顿第二定律求加速度,整体求力;用极限法把F推向两个极端来分析:当F较小(趋近于0)时,由于μ<tanθ,因此物块将沿斜面加速下滑;若F较大(足够大)时,物块将相对斜面向上滑,因此F不能太小,也不能太大,根据牛顿第二定律,运用整体隔离法求出F的取值范围
解答 解:(1)由题意对物体受力分析,重力支持力,由牛顿第二定律的:
mgtan37°=ma°
加速度为:a=gtan37°=7.5N,
整体牛顿第二定律有:
F=(m+M)a=(0.2+1)×7.5=9N
方向水平
若斜面粗糙,水平力F为9N时,物体与斜面仍保持相对静止,此时物体受到的摩擦力为0
若斜面粗糙,水平力F为12N时,整体牛顿第二定律有:
F=(m+M)a
代入数据得:a=$\frac{12}{1+0.2}$=10m/s2
物体与斜面仍保持相对静止,此时物体受到的摩擦力f=macos37°=0.2×10×0.8=1.6N 方向沿斜面向下
若斜面粗糙,水平力F为6N时,整体牛顿第二定律有:
F=(m+M)a
代入数据解得:a=$\frac{6}{1+0.2}$=5m/s2
物体与斜面仍保持相对静止,此时
mgsin37°-f=macos37°
物体受到的摩擦力f=0.4N
答:应对施加一个9N大的水平力F,方向水平
若斜面粗糙,水平力F为9N时,物体与斜面仍保持相对静止,此时物体受到的摩擦力0.
若斜面粗糙,水平力F为12N时,物体与斜面仍保持相对静止,此时物体受到的摩擦力1.6N.
若斜面粗糙,水平力F为6N时,物体与斜面仍保持相对静止,时物体受到的摩擦力0.4N
点评 解决本题的关键能够正确地受力分析,抓住临界状态,运用牛顿第二定律进行求解,注意整体法和隔离法的运用

练习册系列答案
相关题目
10. 如图所示带连个平行金属板水平放置,从紧靠上极板的左边缘以水平初速度v0射入一个带正电的粒子a,该粒子落在下极板的中点,从同一位置以相同的初速度v0水平射入一个质量相等的粒子b,该粒子落在下极板的右边缘(粒子的重力不计).下列说法正确的是( )
如图所示带连个平行金属板水平放置,从紧靠上极板的左边缘以水平初速度v0射入一个带正电的粒子a,该粒子落在下极板的中点,从同一位置以相同的初速度v0水平射入一个质量相等的粒子b,该粒子落在下极板的右边缘(粒子的重力不计).下列说法正确的是( )
 如图所示带连个平行金属板水平放置,从紧靠上极板的左边缘以水平初速度v0射入一个带正电的粒子a,该粒子落在下极板的中点,从同一位置以相同的初速度v0水平射入一个质量相等的粒子b,该粒子落在下极板的右边缘(粒子的重力不计).下列说法正确的是( )
如图所示带连个平行金属板水平放置,从紧靠上极板的左边缘以水平初速度v0射入一个带正电的粒子a,该粒子落在下极板的中点,从同一位置以相同的初速度v0水平射入一个质量相等的粒子b,该粒子落在下极板的右边缘(粒子的重力不计).下列说法正确的是( )| A. | a、b两个粒子在极板间运动的时间之比为1:2 | |
| B. | 电场对a、b两个粒子做的功之比为4:1 | |
| C. | 电场对a、b两个粒子做的功平均功率之比为4:1 | |
| D. | 电场对a、b两个粒子做的功平均功率之比为8:1 |
11. 如图是一个半球形碗,内壁光滑,两个质量相等的小球A、B在碗内不同水平面做匀速圆周运动,F代表碗面对球的支持力,v、a、ω 分别代表线速度、加速度、角速度.以下说法正确的是( )
如图是一个半球形碗,内壁光滑,两个质量相等的小球A、B在碗内不同水平面做匀速圆周运动,F代表碗面对球的支持力,v、a、ω 分别代表线速度、加速度、角速度.以下说法正确的是( )
 如图是一个半球形碗,内壁光滑,两个质量相等的小球A、B在碗内不同水平面做匀速圆周运动,F代表碗面对球的支持力,v、a、ω 分别代表线速度、加速度、角速度.以下说法正确的是( )
如图是一个半球形碗,内壁光滑,两个质量相等的小球A、B在碗内不同水平面做匀速圆周运动,F代表碗面对球的支持力,v、a、ω 分别代表线速度、加速度、角速度.以下说法正确的是( )| A. | vA<vB | B. | FA>FB | C. | aA<aB | D. | ωB<ωA |
8.在国际单位制中,力学的单位被选为基本单位的是( )
| A. | 长度单位、质量单位、时间单位 | B. | 时间单位速度单位质量单位 | ||
| C. | 长度单位、速度单位、时间单位 | D. | 重力单位、时间单位路程单位 |