题目内容
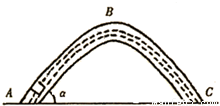
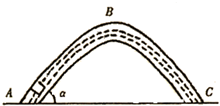 一封闭的弯曲玻璃管处于竖直平面内,其中充满某种液体,内有一个密度为液体密度的
一封闭的弯曲玻璃管处于竖直平面内,其中充满某种液体,内有一个密度为液体密度的| 1 | 2 |
(1)木块到达B点时的速度.
(2)木块从开始运动到最终静止通过的路程.
分析:先求出木块所受浮力的大小,然后根据牛顿第二定律求顶点时的速度,最后由动能定理求总路程
解答:解:(1)设液体的密度为ρ液,木块的密度为ρ木,木块的质量为m,木块的体积为V,则木块所受浮力F浮=ρ液gV=2ρ木gV=2mg
设木块到达B点时的速度为vB,管壁对木块支持力N=(F浮-mg)cosα=mgcosα(F浮-mg)Lsinα-μNL=
mvB2 ①
得:vB=
=2
m/s ②
(2)木块最终只能静止在B处,设木块从开始运动到最终静止通过的路程为s,根据动能定理:
(F浮-mg)Lsinα-μmgcosa?s=0③
得:s=
=3.0m④
答:(1)木块到达B点时的速度为2
m/s.
(2)木块从开始运动到最终静止通过的路程为3.0m.
设木块到达B点时的速度为vB,管壁对木块支持力N=(F浮-mg)cosα=mgcosα(F浮-mg)Lsinα-μNL=
| 1 |
| 2 |
得:vB=
| 2gL(sinα-μcosα) |
| 2 |
(2)木块最终只能静止在B处,设木块从开始运动到最终静止通过的路程为s,根据动能定理:
(F浮-mg)Lsinα-μmgcosa?s=0③
得:s=
| Lsinα |
| μcosα |
答:(1)木块到达B点时的速度为2
| 2 |
(2)木块从开始运动到最终静止通过的路程为3.0m.
点评:本题属于动能定理的综合应用,正确受力分析是关键

练习册系列答案
相关题目

 一封闭的弯曲玻璃管处于竖直平面内,其中充满某种液体,内有一个密度为液体密度的
一封闭的弯曲玻璃管处于竖直平面内,其中充满某种液体,内有一个密度为液体密度的 的木块,从管的A端由静止开始运动,木块与管壁间动摩擦因数μ=0.5,管两臂长AB=BC=L=2m,顶端B处为一小段光滑圆弧,两臂与水平面成α=37°角,如图所示,求:
的木块,从管的A端由静止开始运动,木块与管壁间动摩擦因数μ=0.5,管两臂长AB=BC=L=2m,顶端B处为一小段光滑圆弧,两臂与水平面成α=37°角,如图所示,求:
 的木块,从管的A端由静止开始运动,木块与管壁间动摩擦因数μ=0.5,管两臂长AB=BC=L=2m,顶端B处为一小段光滑圆弧,两臂与水平面成α=37°角,如图所示,求:
的木块,从管的A端由静止开始运动,木块与管壁间动摩擦因数μ=0.5,管两臂长AB=BC=L=2m,顶端B处为一小段光滑圆弧,两臂与水平面成α=37°角,如图所示,求: