题目内容
17.火星探测项目是我国继神舟载人航天工程嫦娥探月工程之后又一个重大太空探索项目,已知地球的质量约为火星质量的10倍,地球的半径约为火星半径的2倍,则下列判断正确的是( )| A. | 同一探测器在火星表面的重力比在地球表面的重力要小 | |
| B. | 火星的第一宇宙速度一定大于地球的第一宇宙速度 | |
| C. | 若探测器绕火星和绕地球做匀速圆周运动的半径相同,则其线速度相同 | |
| D. | 若探测器绕火星和绕地球做匀速圆周运动的半径相同,则其周期相同 |
分析 根据万有引力等于重力,得到g=$\frac{GM}{{R}^{2}}$求解重力加速度之比;根据v=$\sqrt{\frac{GM}{r}}$求解第一宇宙速度之比.
解答 解:A、根据万有引力等于重力得$\frac{GMm}{{R}^{2}}$=mg,
g=$\frac{GM}{{R}^{2}}$
已知地球的质量约为火星质量的10倍,地球的半径约为火星半径的2倍,
则地球的重力加速度与火星的重力加速度之比为5:2.所以同一探测器在火星表面的重力比在地球表面的重力要小,故A正确;
B、第一宇宙速度v=$\sqrt{\frac{GM}{R}}$,已知地球的质量约为火星质量的10倍,地球的半径约为火星半径的2倍,
所以火星的第一宇宙速度一定小于地球的第一宇宙速度,故B错误;
C、根据万有引力提供向心力
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r=m$\frac{{v}^{2}}{r}$
v=$\sqrt{\frac{GM}{r}}$,
已知地球的质量约为火星质量的10倍,探测器绕火星和绕地球做匀速圆周运动的半径相同,所以其线速度不相同,故C错误;
D、T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,已知地球的质量约为火星质量的10倍,探测器绕火星和绕地球做匀速圆周运动的半径相同,所以其周期不相同,故D错误;
故选:A.
点评 本题关键是记住星球表面的重力加速度和第一宇宙速度的表达式,然后代入数据求解即可.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
17.为了减少输电线路中电能损失,发电厂发出的电通常是经过变电所升压后进行远距离输送,再经变电所降压.某变电所将电压u0=11000$\sqrt{2}$sin100πt(V)的交流电降为220V供居民小区用电,则变电所变压器( )
| A. | 原、副线圈匝数比为50:1 | |
| B. | 副线圈中电流的频率是50Hz | |
| C. | 输入电压的最大值为11000V | |
| D. | 输入原线圈的电流等于居民小区各用电器电流的总和 |
8.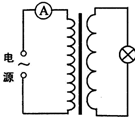 如图所示,理想变压器原、副线圈匝数之比为10:1,原线圈接在频率为50Hz的正弦交流电源上,串接的电流表为理想电流表,副线圈接入“220V 60W”灯泡一只,此时灯泡正常发光.由此可知( )
如图所示,理想变压器原、副线圈匝数之比为10:1,原线圈接在频率为50Hz的正弦交流电源上,串接的电流表为理想电流表,副线圈接入“220V 60W”灯泡一只,此时灯泡正常发光.由此可知( )
 如图所示,理想变压器原、副线圈匝数之比为10:1,原线圈接在频率为50Hz的正弦交流电源上,串接的电流表为理想电流表,副线圈接入“220V 60W”灯泡一只,此时灯泡正常发光.由此可知( )
如图所示,理想变压器原、副线圈匝数之比为10:1,原线圈接在频率为50Hz的正弦交流电源上,串接的电流表为理想电流表,副线圈接入“220V 60W”灯泡一只,此时灯泡正常发光.由此可知( )| A. | 电流表的示数约为0.27A | B. | 原线圈两端电压最大值为2200$\sqrt{2}$V | ||
| C. | 电源的输出功率为6W | D. | 副线圈中交变电流的频率为5Hz |
5.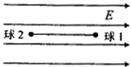 两个质量相同的小球用不可伸长的长为L的绝缘细线连结,置于场强为E的匀强电场中,小球1和小球2均带负电,电量分别为q1和q2(q1>q2),将细线拉直并使之与电场方向平行,如图所示,若将两球同时从静止状态释放,则释放后细线中的张力T为( )(不计重力,线长L远大于小球的线度)
两个质量相同的小球用不可伸长的长为L的绝缘细线连结,置于场强为E的匀强电场中,小球1和小球2均带负电,电量分别为q1和q2(q1>q2),将细线拉直并使之与电场方向平行,如图所示,若将两球同时从静止状态释放,则释放后细线中的张力T为( )(不计重力,线长L远大于小球的线度)
 两个质量相同的小球用不可伸长的长为L的绝缘细线连结,置于场强为E的匀强电场中,小球1和小球2均带负电,电量分别为q1和q2(q1>q2),将细线拉直并使之与电场方向平行,如图所示,若将两球同时从静止状态释放,则释放后细线中的张力T为( )(不计重力,线长L远大于小球的线度)
两个质量相同的小球用不可伸长的长为L的绝缘细线连结,置于场强为E的匀强电场中,小球1和小球2均带负电,电量分别为q1和q2(q1>q2),将细线拉直并使之与电场方向平行,如图所示,若将两球同时从静止状态释放,则释放后细线中的张力T为( )(不计重力,线长L远大于小球的线度)| A. | T=(q2-q1)E+$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$ | B. | T=$\frac{1}{2}$(q2-q1)E+$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$ | ||
| C. | T=$\frac{1}{2}$(q2-q1)E-$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$ | D. | T=(q2+q1)E+$\frac{k{q}_{1}{q}_{2}}{{L}^{2}}$ |
2.关于物理学的研究方法,以下说法正确的是( )
| A. | 建立质点和瞬时速度概念时,应用了微元法 | |
| B. | 伽利略开创了运用逻辑推理和实验相结合进行科学研究的方法 | |
| C. | 卡文迪许在利用扭秤实验装置测量万有引力常量时,应用了等效替代的方法 | |
| D. | 电流是用电压和电阻的比值定义的,因而通过导体的电流与导体两端的电压成正比与导体的电阻成反比 |
7.通过观测发现某星球半径是地球半径的k倍,绕该星球近地运行卫星的周期是地球近地卫星周期的n倍,下列说法中错误的是( )
| A. | 绕该星球近地运行卫星的速度是地球近地卫星速度的$\frac{k}{n}$ | |
| B. | 该星球的质量是地球质量的$\frac{{k}^{3}}{{n}^{2}}$ | |
| C. | 该星球表面的重力加速度是地球表面的重力加速度的$\frac{k}{{n}^{2}}$ | |
| D. | 该星球的密度是地球密度的$\frac{k}{{n}^{2}}$ |

 某同学利用如图所示的装置探究功与速度变化的关系.
某同学利用如图所示的装置探究功与速度变化的关系.