题目内容
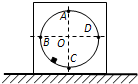 质量为M的物体内有光滑的圆形竖直轨道,现有一质量为m的小滑块在该圆形轨道内沿顺时针做圆周运动,A、C分别为圆周的最高点和最低点,B、D点与圆心O在同一条水平线上,小滑块运动时,物体M在水平地面上静止不动.有关物体M对地面的压力N和地面对物体M的摩擦力的说法正确的是(当地的重力加速度为g)
质量为M的物体内有光滑的圆形竖直轨道,现有一质量为m的小滑块在该圆形轨道内沿顺时针做圆周运动,A、C分别为圆周的最高点和最低点,B、D点与圆心O在同一条水平线上,小滑块运动时,物体M在水平地面上静止不动.有关物体M对地面的压力N和地面对物体M的摩擦力的说法正确的是(当地的重力加速度为g)
- A.小滑块在A点时,N>Mg,摩擦力方向向左
- B.小滑块在B点时,N=Mg,摩擦力方向向右
- C.小滑块在C点时,N<(M+m)g,与地面无摩擦力
- D.小滑块在D点时,N=(M+m)g,摩擦力方向向左
B
分析:小滑块在竖直面内做圆周运动,小滑块的重力和圆形轨道对滑块的支持力的合力作为向心力,根据在不同的地方做圆周运动的受力,可以分析得出物体M对地面的压力N和地面对物体M的摩擦力的大小.
解答:A、小滑块在A点时,滑块对M的作用力在竖直方向上,系统在水平方向不受力的作用,所以没有摩擦力的作用,所以A错误.
B、小滑块在B点时,需要的向心力向右,所以M对滑块有向右的支持力的作用,对M受力分析可知,地面要对物体有向右的摩擦力的作用,在竖直方向上,由于没有加速度,物体受力平衡,所以物体M对地面的压力N=Mg,所以B正确.
C、小滑块在C点时,滑块的向心力向上,所以C对物体M的压力要大于C的重力,故M受到的滑块的压力大于mg,那么M对地面的压力就要大于(M+m)g,所以C错误.
D、小滑块在D点和B的受力的类似,由B的分析可知,D错误.
故选B.
点评:小滑块做圆周运动,分析清楚小滑块做圆周运动的向心力的来源,即可知道小滑块和M之间的作用力的大小,再由牛顿第三定律可以分析得出地面对M的作用力.
分析:小滑块在竖直面内做圆周运动,小滑块的重力和圆形轨道对滑块的支持力的合力作为向心力,根据在不同的地方做圆周运动的受力,可以分析得出物体M对地面的压力N和地面对物体M的摩擦力的大小.
解答:A、小滑块在A点时,滑块对M的作用力在竖直方向上,系统在水平方向不受力的作用,所以没有摩擦力的作用,所以A错误.
B、小滑块在B点时,需要的向心力向右,所以M对滑块有向右的支持力的作用,对M受力分析可知,地面要对物体有向右的摩擦力的作用,在竖直方向上,由于没有加速度,物体受力平衡,所以物体M对地面的压力N=Mg,所以B正确.
C、小滑块在C点时,滑块的向心力向上,所以C对物体M的压力要大于C的重力,故M受到的滑块的压力大于mg,那么M对地面的压力就要大于(M+m)g,所以C错误.
D、小滑块在D点和B的受力的类似,由B的分析可知,D错误.
故选B.
点评:小滑块做圆周运动,分析清楚小滑块做圆周运动的向心力的来源,即可知道小滑块和M之间的作用力的大小,再由牛顿第三定律可以分析得出地面对M的作用力.

练习册系列答案
相关题目
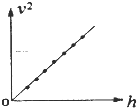 (1)为探究物体下落过程中机械能是否守恒,采用实验装置如图所示.已知重力加速度大小为g
(1)为探究物体下落过程中机械能是否守恒,采用实验装置如图所示.已知重力加速度大小为g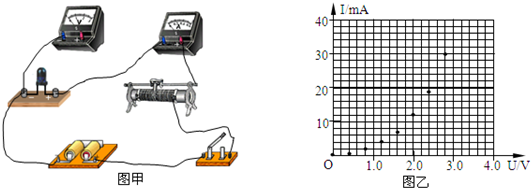
 (2009?宁夏)[物理-选修3-5]
(2009?宁夏)[物理-选修3-5]



