题目内容
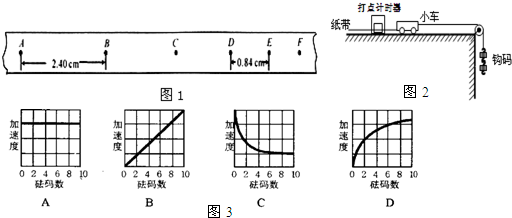
(1)图1是一辆连有纸带的小车做匀变速直线运动时,打点计时器所打的纸带的一部分.打点频率为50Hz,图中A、B、C、D、E、F…是按时间顺序先后确定的计数点(每两个计数点间有四个实验点未画出).用刻度尺量出AB、DE之间的距离分别是2.40cm和0.84cm,①那么小车的加速度大小是 m/s2,方向与小车运动的方向相 .②若当时电网中交变电流的频率变为60Hz电压变为210V,但该同学并不知道,那么做实验的这个同学测得的物体加速度的测量值与实际值相比 (选填:“偏大”、“偏小”或“不变”).
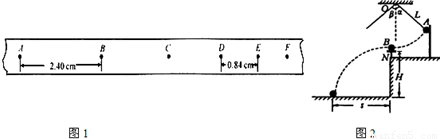
(2)某同学在验证牛顿第二定律的实验中,实验装置如图2所示.打点计时器使用的交流电源的频率为50Hz.开始实验时,细线上挂适当的钩码,释放小车后,小车做匀加速运动,与小车相连的纸带上被打出一系列小点.
①实验中,该同学测出拉力F(钩码重力)和小车质量M,根据
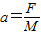 计算出加速度.发现绝大多数情况下,根据公式计算出的加速度要比利用纸带测出的加速度大.若该同学实验操作过程没有错误,试分析其原因.(至少写两点)
计算出加速度.发现绝大多数情况下,根据公式计算出的加速度要比利用纸带测出的加速度大.若该同学实验操作过程没有错误,试分析其原因.(至少写两点)、 .
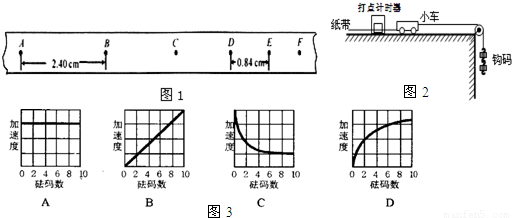
②另一同学在完成同样的实验时,每次实验在吊挂之处逐次增加一个质量为50g的砝码,利用纸带测出每次小车的加速度,如果小车质量为100g,细绳质量可忽略,则如图3,下列曲线何者最适合描述小车加速度随着吊挂砝码个数的变化 .
【答案】分析:(1)纸带实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的加速度.
(2)①实验中小车合力要小于钩码重力,所以根据公式计算出的加速度要比利用纸带测出的加速度大.
②根据牛顿第二定律表示出加速度求解.
解答:解:(1)①每两个计数点间有四个实验点未画出,所以相邻的计数点之间的时间间隔为0.1s
根据运动学公式得:△x=at2,
a=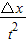 =
=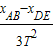 =0.52m/s2,
=0.52m/s2,
由于从A到F相邻的计数点位移逐渐减小,所以纸带做减速运动,加速度方向与小车运动的方向相反.
②如果在某次实验中,交流电的频率偏离60Hz,那么实际打点周期变小,
根据运动学公式△x=at2得:真实的加速度值就会偏大,
所以测量的加速度值与真实的加速度值相比是偏小
(2)①实验中小车合力要小于钩码重力,所以根据公式计算出的加速度要比利用纸带测出的加速度大的原因是存在摩擦阻力,绳实际的拉力小于钩码的重力.
所以原因为:没有平衡摩擦力,或钩码质量没有远小于M
②根据牛顿第二定律得:
对m:mg-F拉=ma
对M:F拉=Ma
解得:F拉=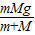
所以小车加速度a=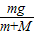 =
=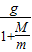
每次实验在吊挂之处逐次增加一个质量为50g的砝码,即m增大,
所以描述小车加速度随着吊挂砝码个数的变化最为适合是D,
故答案为:(1)①0.52 相反 ②偏小 (2)①没有平衡摩擦力 钩码质量没有远小于M ②D
点评:要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.
解决实验问题首先要掌握该实验原理,了解实验的操作步骤和数据处理以及注意事项,同时要熟练应用所学基本规律解决实验问题.
(2)①实验中小车合力要小于钩码重力,所以根据公式计算出的加速度要比利用纸带测出的加速度大.
②根据牛顿第二定律表示出加速度求解.
解答:解:(1)①每两个计数点间有四个实验点未画出,所以相邻的计数点之间的时间间隔为0.1s
根据运动学公式得:△x=at2,
a=
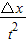 =
=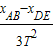 =0.52m/s2,
=0.52m/s2,由于从A到F相邻的计数点位移逐渐减小,所以纸带做减速运动,加速度方向与小车运动的方向相反.
②如果在某次实验中,交流电的频率偏离60Hz,那么实际打点周期变小,
根据运动学公式△x=at2得:真实的加速度值就会偏大,
所以测量的加速度值与真实的加速度值相比是偏小
(2)①实验中小车合力要小于钩码重力,所以根据公式计算出的加速度要比利用纸带测出的加速度大的原因是存在摩擦阻力,绳实际的拉力小于钩码的重力.
所以原因为:没有平衡摩擦力,或钩码质量没有远小于M
②根据牛顿第二定律得:
对m:mg-F拉=ma
对M:F拉=Ma
解得:F拉=
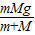
所以小车加速度a=
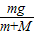 =
=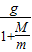
每次实验在吊挂之处逐次增加一个质量为50g的砝码,即m增大,
所以描述小车加速度随着吊挂砝码个数的变化最为适合是D,
故答案为:(1)①0.52 相反 ②偏小 (2)①没有平衡摩擦力 钩码质量没有远小于M ②D
点评:要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.
解决实验问题首先要掌握该实验原理,了解实验的操作步骤和数据处理以及注意事项,同时要熟练应用所学基本规律解决实验问题.

练习册系列答案
相关题目

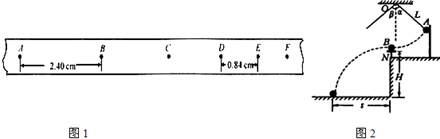 (1)图1是一辆连有纸带的小车做匀变速直线运动时,打点计时器所打的纸带的一部分.打点频率为50Hz,图中A、B、C、D、E、F…是按时间顺序先后确定的计数点(每两个计数点间有四个实验点未画出).用刻度尺量出AB、DE之间的距离分别是2.40cm和0.84cm.
(1)图1是一辆连有纸带的小车做匀变速直线运动时,打点计时器所打的纸带的一部分.打点频率为50Hz,图中A、B、C、D、E、F…是按时间顺序先后确定的计数点(每两个计数点间有四个实验点未画出).用刻度尺量出AB、DE之间的距离分别是2.40cm和0.84cm.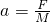 计算出加速度.发现绝大多数情况下,根据公式计算出的加速度要比利用纸带测出的加速度大.若该同学实验操作过程没有错误,试分析其原因.(至少写两点)
计算出加速度.发现绝大多数情况下,根据公式计算出的加速度要比利用纸带测出的加速度大.若该同学实验操作过程没有错误,试分析其原因.(至少写两点)