题目内容
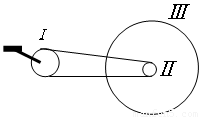
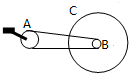如图所示，是自行车传动结构的示意图，其中有齿轮A、B和链条及车轮C，假设脚踏板使齿轮A每n秒转一圈，要知道在这种情况下自行车的行驶速度，则①还需测量哪些物理量
大齿轮A的半径r1
大齿轮A的半径r1
、小齿轮的半径r2
小齿轮的半径r2
、后轮半径r3
后轮半径r3
；②自行车的行驶速度是多少？（用你假设的物理量表示）
| 2πr1r3 |
| nr2 |
| 2πr1r3 |
| nr2 |
分析：根据大齿轮的周期求出大齿轮的角速度．大齿轮和小齿轮靠链条传动，边缘点线速度相等，根据半径关系可以求出小齿轮的角速度．后轮与小齿轮具有相同的角速度，若要求出自行车的速度，需要测量后轮的半径，抓住角速度相等，求出自行车的速度．
解答：解：①要知道自行车的行驶速度，还需测量：大齿轮A的半径r1，小齿轮的半径r2，后轮半径r3．
②大齿轮的周期为n秒，则大齿轮的角速度ω1=
=
rad/s．
大齿轮和小齿轮的线速度相等，小齿轮与后轮的角速度相等．
因为ω1r1=ω2r2，所以ω2=
．
后轮的角速度与小齿轮的角速度相等，所以线速度v=r3ω2=
=
．
故答案为：①大齿轮A的半径r1，小齿轮的半径r2，后轮半径r3．②
．
②大齿轮的周期为n秒，则大齿轮的角速度ω1=
| 2π |
| T |
| 2π |
| n |
大齿轮和小齿轮的线速度相等，小齿轮与后轮的角速度相等．
因为ω1r1=ω2r2，所以ω2=
| ω1r1 |
| r2 |
后轮的角速度与小齿轮的角速度相等，所以线速度v=r3ω2=
| ω1r1r3 |
| r2 |
| 2πr1r3 |
| nr2 |
故答案为：①大齿轮A的半径r1，小齿轮的半径r2，后轮半径r3．②
| 2πr1r3 |
| nr2 |
点评：解决本题的关键知道靠链条传动，线速度相等，共轴转动，角速度相等．
练习册系列答案
相关题目
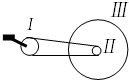如图所示，是自行车传动结构的示意图．其中Ⅰ是大齿轮，Ⅱ是小齿轮，Ⅲ是后轮．
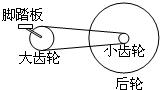如图所示，是自行车传动结构的示意图，假设脚踏板每n秒转一圈，要知道这种情况下自行车的行驶速度，则：
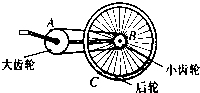如图所示，是自行车传动机构的示意图．已知大齿轮A、小齿轮B与后轮C的半径分别是r1、r2、r3，若脚踏板的转速为n，自行车在平直路面上行驶，求：