题目内容
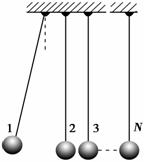
某兴趣小组设计了一种实验装置,用来研究碰撞问题,其模型如右图所示。用完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平杆,球间有微小间隔,从左到右,球的编号依次为1、2、3…….N,球的质量依次递减,每个球的质量与其相邻左球质量之比为k(k<1)。将1号球向左拉起,然后由静止释放,使其与2号球碰撞,2号球再与3号球碰撞……所有碰撞皆为无机械能损失的正碰。并假设所有的球作为主动球完成一次碰撞后均由于某种原因与绳脱离并作自由落体运动。(不计空气阻力,忽略绳的伸长,g取10 m/s2)
(1)设与n+1号球碰撞前,n号球的速度为vn,求n+1号球被碰撞后瞬间的速度。
(2)若N=5,在1号球向左拉高h的情况下,要使5号球碰撞后升高16h(16h小于绳长),问k值为多少?
解析:(1)设n号球质量为mn,n+1号球质量为mn+1,碰撞后的速度分别为v n′、vn+1′,取水平向右为正方向,据题意有n号球与n+1号球碰撞前的速度分别为vn、0,且
mn+1=kmn
根据动量守恒定律,有
mnvn=mnvn′n+kmnv n+1′ ①
根据机械能守恒定律,有
![]() mnvn2=
mnvn2=![]() mnv n′2+
mnv n′2+![]() kmnv n+1′2 ②
kmnv n+1′2 ②
由①②得
v n+1′=![]() (v n+1′=0舍去)
(v n+1′=0舍去)
(2)设1号球摆至最低点时的速度为v1,由机械能守恒定律有
m1gh=![]() m1v12 ④
m1v12 ④
解得 v1=![]() ⑤
⑤
同理可求5号球碰后瞬间的速度
v5=![]() ⑥
⑥
设n+1号球与n+2号球碰前的速度为vn+1
据题意有vn+1=v n+1′[
vn+1=![]() nv1 ⑦ ks5u
nv1 ⑦ ks5u
N=n+1=5时,
v5=(![]() )4v1 ⑧
)4v1 ⑧
由⑤⑥⑧三式得 k=![]() -1≈0.414(k=-
-1≈0.414(k=-![]() -1舍去) ⑨
-1舍去) ⑨

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案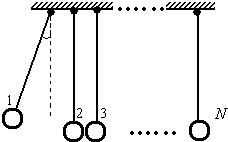 某兴趣小组设计了一种实验装置,用来研究碰撞问题,其模型如图所示不用完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平杆、球间有微小间隔,从左到右,球的编号依次为1、2、3…N,球的质量依次递减,每球质量与其相邻左球质量之比为k(k<1).将1号球向左拉起,然后由静止释放,使其与2号球碰撞,2号球再与3号球碰撞…所有碰撞皆为无机械能损失的正碰.(不计空气阻力,忽略绳的伸长,g取10m/s2)
某兴趣小组设计了一种实验装置,用来研究碰撞问题,其模型如图所示不用完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平杆、球间有微小间隔,从左到右,球的编号依次为1、2、3…N,球的质量依次递减,每球质量与其相邻左球质量之比为k(k<1).将1号球向左拉起,然后由静止释放,使其与2号球碰撞,2号球再与3号球碰撞…所有碰撞皆为无机械能损失的正碰.(不计空气阻力,忽略绳的伸长,g取10m/s2) (2012?江苏)某兴趣小组设计了一种发电装置,如图所示.在磁极和圆柱状铁芯之间形成的两磁场区域的圆心角α均为
(2012?江苏)某兴趣小组设计了一种发电装置,如图所示.在磁极和圆柱状铁芯之间形成的两磁场区域的圆心角α均为 π,磁场均沿半径方向,匝数为N的矩形线圈.abcd的边长ab=cd=l、bc=ad=2l.线圈以角速度ω绕中心轴匀速转动、bc和ad边同时进入磁场,在磁场中,两条边所经过处的磁感应强度大小均为B、方向始终与两条边的运动方向垂直,线圈的总电阻为r,外接电阻为R.求:
π,磁场均沿半径方向,匝数为N的矩形线圈.abcd的边长ab=cd=l、bc=ad=2l.线圈以角速度ω绕中心轴匀速转动、bc和ad边同时进入磁场,在磁场中,两条边所经过处的磁感应强度大小均为B、方向始终与两条边的运动方向垂直,线圈的总电阻为r,外接电阻为R.求:
