题目内容
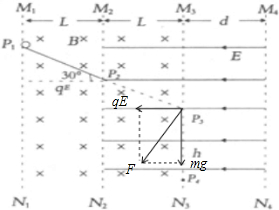
 如图所示,四个竖直的分界面间的距离分别为L、L和d,在分界面M1N1-M3N3之间存在水平向里的匀强磁场,在分界面M2N2-M4N4之间存在水平向左的匀强电场,一倾角为30°的光滑斜面,其上、下端P1和P2正好在分界面上.一质量为m,带电荷量为q的小球在P1点由静止开始沿斜面下滑(电荷量不变),重力加速度为g.
如图所示,四个竖直的分界面间的距离分别为L、L和d,在分界面M1N1-M3N3之间存在水平向里的匀强磁场,在分界面M2N2-M4N4之间存在水平向左的匀强电场,一倾角为30°的光滑斜面,其上、下端P1和P2正好在分界面上.一质量为m,带电荷量为q的小球在P1点由静止开始沿斜面下滑(电荷量不变),重力加速度为g.(1)求小球运动到斜面底端P2时的速度v大小
(2)已知小球离开斜面底端P2后,做直线运动到分界面M3N3上的P3点,求空间电场强度E和磁感应强度B.的大小;
(3)已知d足够大,小球离开P3点后将从P4点再次经过M3N3面,求P3和P4两点间的距离h.
分析:(1)小球在斜面上下滑的过程中只有重力做功,根据动能定理可求滑至斜面底端的速度大小;
(2)根据小球做直线运动,因为存在磁场故只能做匀速直线运动,根据合力为零由平衡条件求解;
(3)离开P3时,小球所受合力与速度方向垂直,故小球做类平抛运动,根据类平抛运动知识求解P3P4两点间的距离
(2)根据小球做直线运动,因为存在磁场故只能做匀速直线运动,根据合力为零由平衡条件求解;
(3)离开P3时,小球所受合力与速度方向垂直,故小球做类平抛运动,根据类平抛运动知识求解P3P4两点间的距离
解答:解:(1)小球在斜面上运动时受重力支持力和洛伦兹力作用,因为支持力和洛伦兹力都速度方向垂直不做功,固合外力做即为重力做功,根据运动定理有:
mgLtan30°=
mv2-0
解得:v=
(2)小球从P2到P3点做直线运动,因为重力和电场力均为恒力,而F洛=qvB只能是做匀速直线运动,所受合力为零,由平衡条件有:
qE=qBvsin30° ①
mg=qBvcos30° ②
联立①②解处:E=
,B=
(3)由(2)分析知,从P2到P3点做直线运动,合力为零,因为洛伦兹力始终与速度方向垂直,所以重力和电场力的合力与速度方向垂直.
所以小球从P3到P4点做类平抛运动,在P3点速度为v,沿P2P3方向做匀速运动,与此方向垂直的方向为匀加速运动,则:
小球做类平抛运动的加速度为a,则有:
=ma
得a=
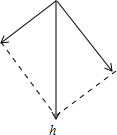
hsin30°=vt
hcos30°=
at2
代入数据得:h=4
L
答:(1)小球运动到斜面底端P2时的速度v=
(2)已知小球离开斜面底端P2后,做直线运动到分界面M3N3上的P3点,求空间电场强度E和磁感应强度B的大小为B=
;
(3)已知d足够大,小球离开P3点后将从P4点再次经过M3N3面,P3和P4两点间的距离h=4
L.
mgLtan30°=
| 1 |
| 2 |
解得:v=
|
(2)小球从P2到P3点做直线运动,因为重力和电场力均为恒力,而F洛=qvB只能是做匀速直线运动,所受合力为零,由平衡条件有:
qE=qBvsin30° ①
mg=qBvcos30° ②
联立①②解处:E=
| ||
| 3q |
| m |
| q |
|
(3)由(2)分析知,从P2到P3点做直线运动,合力为零,因为洛伦兹力始终与速度方向垂直,所以重力和电场力的合力与速度方向垂直.
所以小球从P3到P4点做类平抛运动,在P3点速度为v,沿P2P3方向做匀速运动,与此方向垂直的方向为匀加速运动,则:

小球做类平抛运动的加速度为a,则有:
| mg |
| cos30° |
得a=
| 2g | ||
|

hsin30°=vt
hcos30°=
| 1 |
| 2 |
代入数据得:h=4
| 3 |
答:(1)小球运动到斜面底端P2时的速度v=
|
(2)已知小球离开斜面底端P2后,做直线运动到分界面M3N3上的P3点,求空间电场强度E和磁感应强度B的大小为B=
| m |
| q |
|
(3)已知d足够大,小球离开P3点后将从P4点再次经过M3N3面,P3和P4两点间的距离h=4
| 3 |
点评:洛伦兹力始终与速度垂直,对粒子始终不做功,在重力场和电场以及磁场复合场中做直线运动,粒子只能做匀速直线运动.能根据类平抛运动的条件判断物体在电场和重力场作用下做类平抛运动是解决本题的关键.

练习册系列答案
相关题目



